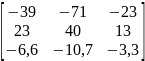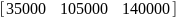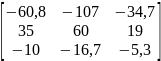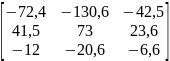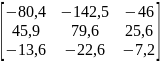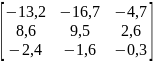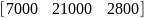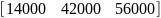- •Предисловие
- •Краткое введение в matlab и Simulink
- •Лабораторная работа № 1 определение параметров динамических характеристик линейных звеньев систем автоматического управления
- •Краткие теоретические сведения
- •Типовые динамические звенья
- •Порядок выполнения работы
- •Содержание отчета
- •Методический пример по использованию пакета
- •Главное окно системы matlab
- •Результат выполнения команды step (переходная характеристика)
- •Результат выполнения команды impulse (импульсная характеристика)
- •Исследование реакции нескольких звеньев
- •Модель Simulink с подготовленной для линейного анализа схемой
- •Окно отображение результатов процесса линеаризации
- •Результаты линейного анализа
- •Результаты линейного анализа в окне «Figure».
- •Формат сохраняемого графического материала Контрольные вопросы
- •Лабораторная работа № 2 исследование преобразований структурных схем
- •Краткие теоретические сведения
- •Описание системы управления сигнальным графом
- •Использование пакета MatLab
- •Порядок выполнения работы
- •Содержание отчета
- •Методический пример в Matlab
- •Модель сау
- •Преобразованная модель сау
- •Контрольные вопросы
- •Лабораторная работа № 3 исследование устойчивости и качества линейной системы автоматического управления
- •Порядок выполнения работы
- •Пояснения к выполнению работы
- •Содержание отчета
- •Методический пример в Matlab
- •Исследование сау с п-регулятором
- •Результаты моделирования переходной функции сау для разных значений коэффициента пропорционального регулятора.
- •Ошибка регулирования при значениях п-регулятора (1, 2, 5, 10, 25, 50), увеличивающегося сверху вниз.
- •Ошибка регулирования при изменении значения п-регулятора Исследование сау с и и пи-регуляторами
- •Переходная характеристика сау
- •Ошибка регулирования сау
- •Увеличение колебательности выходного сигнала с ростом Ки
- •Результаты моделирования
- •Изменение выходного сигнала с ростом к
- •Контрольные вопросы
- •Лабораторная работа № 4 метод корневого годографа
- •Краткие теоретические сведения
- •Порядок выполнения работы
- •Содержание отчета
- •Методический пример в Matlab
- •Контрольные вопросы
- •Лабораторная работа № 5 исследование замкнутых систем автоматического управления с жесткой обратной связью
- •Краткие теоретические сведения
- •Способы коррекции сау
- •Порядок выполнения работы
- •Структурная схема объекта регулирования
- •Содержание отчета
- •Методический пример в Matlab
- •Результаты линейного анализа скорректированной сау. Контрольные вопросы
- •Лабораторная работа № 6 исследование пид регуляторов
- •Краткие теоретические сведения
- •Использование пакета MatLab
- •Порядок выполнения работы
- •Содержание отчета
- •Контрольные вопросы
- •Лабораторная работа № 7 исследование фазовых портретов линейных систем автоматического управления
- •Порядок выполнения работы
- •Пример моделирования
- •Содержание отчета
- •Контрольные вопросы
- •Лабораторная работа № 8 модальное управление
- •Краткие теоретические сведения
- •Использование MatLab
- •Порядок выполнения работы
- •Модели в пространстве состояний
- •Содержание отчета
- •Контрольные вопросы
- •Лабораторная работа № 9 наблюдающие устройства
- •Краткие теоретические сведения
- •Использование пакета MatLab
- •Порядок выполнения работы
- •Содержание отчета
- •Контрольные вопросы
- •Список рекомендуемой литературы
Использование MatLab
В программном комплексе MatLab для формирования модели в пространстве состояний используется функция ss,
>> w1 = ss(A, B, C, D),
где A, B, C, D – матрицы модели.
Из модели в пространстве состояний можно получить ПФ команn дой:
>> w2 = tf(w1)
И, наоборот, если уже существует модель, заданная ПФ, то ее можn но преобразовать в пространство состояний с помощью команды ss:
>> w=tf([2 2],[3 4 1]);
>> w1=ss(w)
Заметим, что одной и той же ПФ могут, вообще говоря, соответn ствовать разные модели в пространстве состояний, но всем этим моделям соответствует одна и та же ПФ.
Матрица управляемости может быть построена с помощью функn ции ctrb, которая вызывается одной из команд:
>> W = ctrb(A, B)
>> W = ctrb(sys)
>> W = ctrb(sys.A, sys.B)
В пакете MatLab имеется функция acker, с помощью которой можно обеспечить желаемое расположение полюсов одномерной линейной системы (в соответствии с формулой Аккермана):
>> k = acker(A,B,P),
где А и В – матрицы системы; Р – вектор, задающий желаемое распоn ложение полюсов системы.
Пример. Пусть система описывается матрицами
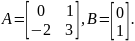
Желаемые полюса заданы вектором:

Тогда рассчитать значение коэффициентов обратных связей можно с помощью команд
>>A=[0 1;,2 3];
>> B=[0; 1];
>> P=[,1 ,3];
>> K=acker(A,B,P)
K = 1 7
Таким образом, управление в этом примере должно быть сформировано в виде

Для многомерных систем в пакете MatLab имеется функция place (ее можно использовать также и для одномерных систем). Функция
>> K=place(A,B,P)
рассчитывает матрицу коэффициентов обратных связей K, которая обеспечивает желаемое расположение полюсов системы. Длина вектора P должна быть равна числу строк матрицы А.
Следует
заметить, что метод модального управления
не гарантирует равенство установившейся
ошибки нулю. Для обеспечения равенства
задающего воздействия и выходного
сигнала системы в установившемся режиме
вводится масштабирующий коэффициент
 .
Для
его
вычисления запишем уравнения состояния
в виде:
.
Для
его
вычисления запишем уравнения состояния
в виде:
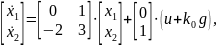
подставляя уравнение (6), имеем:
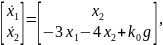

В установившемся режиме получаем
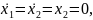
и должно выполняться условие

Следовательно, из уравнения (7) получаем
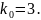
На этот коэффициент должно умножаться входное воздействие.
В пакете моделирования Simulink MatLab для описания объекта в пространстве состояний имеется блок State Space. Однако этот блок не позволяет непосредственно оценивать текущее значение вектора состояния, поэтому для моделирования работы модального регулятор нужно детально описывать матричные операции.
Порядок выполнения работы
1. Для полученного варианта объекта управления, заданного матрицами А, В, С (см. табл.), обосновать возможность модального управления с помощью критерия управляемости.
2. Рассчитать коэффициенты обратной связи, при которой обеспечивается желаемое расположение полюсов замкнутой системы. Рассмотреть два варианта - когда перерегулирование равно 30 и 0% (апериодический процесс).
Таблица
Модели в пространстве состояний
№ |
А |
В |
С |
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
|
11 |
|
|
|
12 |
|
|
|
3. С помощью выбора масштабирующего коэффициента обеспечить в системе нулевую установившуюся ошибку.
4. Собрать в Simulink MatLab структурную схему системы с модальным регулятором (не используя блок State space) и проверить полученные результаты.