- 12 -

Калинин Б.Н.

Глава10 Жесткие уравнения

Содержание

Калинин Б.Н. 1

Глава10 1

Жесткие уравнения 1

Содержание 1

10.1. Примеры жестких уравнений 2

10.2. Определение жестких систем уравнений 5

10.3. Абсолютная и условная устойчивость разностных методов 5

10.4. Область устойчивости 6

10.5. Чисто неявные методы 8

10.1. Примеры жестких уравнений

Устойчивый разностный метод решения задачи Коши

должен удовлетворять условию корней:

Все корни характеристического уравнения

должны лежать внутри или на границе единичного круга комплексной плоскости, причем на границе круга не должно быть кратных корней.

Однако условие корней не учитывает коэффициенты правой части уравнения, описывающего разностный метод, и вследствие этого не учитывает характерных свойств решения исходной дифференциальной задачи. Существует класс задач, для решения которых требуется значительно меньший шаг, чем это казалось бы из вида решения.

Пример 10.1 Рассмотрим задачу Коши Это линейное уравнение первого порядка. Легко найти точное решение задачи Коши:

Э кспоненциальное слагаемое точного решения быстро затухает: уже при . Можно ожидать, что для будет допустима величина шага . Найдем с помощью метода Рунге-Кутта четвертого порядка значение . Точное значение равно . Решение в среде Mahtcad для четырех значений шага h показано на рис 10.1. Оказывается, что метод Рунге-Кутта перестает работать уже при величине шага .

Пример 10.2 Рассмотрим задачу Коши для системы уравнений :

Общее решение этой системы уравнений имеет вид:

.

Решение данной начальной задачи равно

.

Точное решение данной задачи в точке равно: . С помощью метода Рунге-Кутта найдем приближенное решение в этой точке. Решение в среде Mahtcad для четырех значений шага приращения аргумента (или, иначе, для четырех значений числа шагов, необходимых для прихода в точку ) показано на рис 10.2. Видим, что метод Рунге-Кутта перестает работать при значении шага . Это очень малый шаг для описания экспоненты . Правда, общее решение содержит быстро меняющуюся составляющую , однако в решении данной конкретной задачи Коши эта составляющая отсутствует.

Рассмотренные примеры имеют общую черту – описывают процессы, сильно отличающиеся по скорости изменения. Описанные ранее методы решения требуют учета наискорейшего процесса даже там, где соответствующее слагаемое в точном решении пренебрежимо мало. Подобные задачи, встречающиеся при моделировании химических реакций, электронных схем, систем управления и др., называются жесткими задачами.

Пример 10.3. Проанализируем механизм возникновения неустойчивости при решении задачи Коши для системы уравнений:

(10.1)

Решение этой системы линейных уравнений с постоянными коэффициентами может быть легко найдено аналитически. Общее решение представляет сумму затухающих экспонент:

Постоянные для интегральной кривой, проходящей через точку определяются уравнениями:

(10.2)

В частности, для начальной точки получим:

(10.3)

Решение (10.3) показано на рис.10.3. Точные решения содержат две компоненты: медленно меняющуюся составляющую и быстро затухающую компоненту . Вторая компонента имеет значение 0.018 уже при .

Решим теперь эту задачу Коши явным методом Эйлера, выбрав шаг приращения аргумента :

(10.4)

Результаты вычислений в соответствии с формулами (10.4) приведены в таблице 10.1 и на графике рис. 10.4.

Т аблица 10.1

x	0	0.1	0.2	0.3	0.4	0.5
y	1	4.6	-7.7	28	-80.2	244
z	3	-1.4	10.3	-26	81.8	-242

Видим, что явный метод Эйлера в данном случае оказывается неустойчивым. Рассмотрим более подробно причину неустойчивости. При решении дифференциального уравнения (или системы уравнений) на каждом шаге приращения аргумента происходит переход на новую интегральную кривую. Начальная точка лежит на кривой, являющейся точными решением задачи, но уже точка находится на другой интегральной кривой. Уравнение этой кривой включает новые значения постоянных С, которые определяются формулами (10.2). Константы для точек, вычисляемых по методу Эйлера, приведены в таблице 10.2.

Таблица 10.2

i	0	1	2	3	4
	2	1.95	1.92	1.87	1.82
	1	-164

Н а рис. 10.5 показано приближенное решение и интегральные кривые

,

проходящие через точки . Метод Эйлера означает движение по касательной к интегральной кривой. На первом шаге – это движение по касательной к точному решению исходной задачи из точки в точку . Интегральная кривая, проходящая через эту точку, расположена выше истинного решения начальной задачи. Эта кривая определяется значениями постоянных . Движение по касательной к этой кривой приводит в точку . Движение на следующем шаге уводит за пределы графика и т.д.

Рассмотрим также решение данной задачи Коши с помощью неявного метода Эйлера. Неявный метод Эйлера для уравнения описывается формулой:

, где . (10.5)

Формула (10.5) описывает движение по касательной к интегральной кривой, проходящей через следующую точку . В данном случае мы имеем линейную систему дифференциальных уравнений (10.1), поэтому формула неявного метода:

–

может быть легко разрешена относительно :

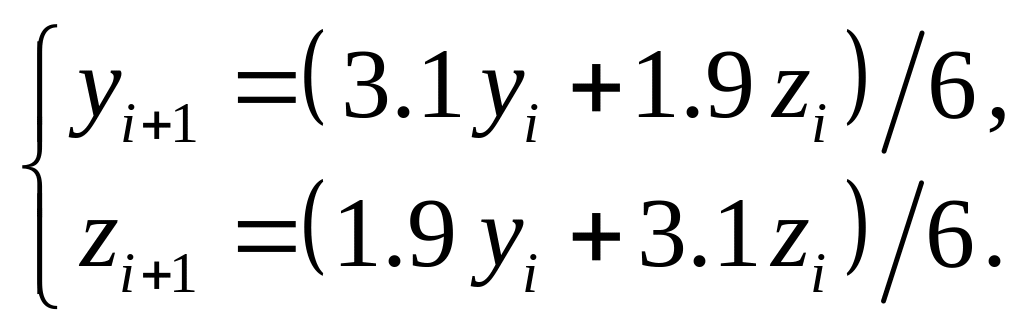(10.6)

Результаты расчетов в соответствии с формулами (10.6) приведены в таблице 10.3 и показаны на графиках.

Таблица 10.3

x	0	0.1	0.2	0.3	0.4	0.5
y	1	1.47	1.35	1.15	0.963	0.803
z	3	1.87	1.43	1.165	0.966	0.804

Н а рис 10.6 показано точное решение начальной задачи (кривые и ) и решение, полученное с помощью неявного метода Эйлера (кривые ). Видно, что неявный метод Эйлера является адекватным способом решения данной задачи.

На рис. 10.7 показано приближенное решение и интегральные кривые, проходящие через последовательные точки . Видно, что неявный метод Эйлера реализует движение по касательной к интегральной кривой, проходящей через следующую точку приближенного решения.