2.3. Десятковий запис наближених чисел. Значуща цифра числа.

Системою числення, або нумерацією, називається сукупність правил, що служать для найменування та позначення чисел.

Цифрами називаються умовні знаки, що використовуються для позначення чисел системи числення.

При запису чисел в десятковій системі числення користуються цифрами 0, 1, 2, …, 9. Система являється позиційною. Так число 4444,44 має шість цифр 4, але всі вони мають різні значення. Це число є скороченим записом суми

В десятковому числі одиниця кожного розряду дорівнює десяти одиницям попереднього розряду. При вирішенні задач часто ставиться умова: обчислити результат з точністю до 0,1; 0,01; тощо. Це не зовсім вірно, тому що число десяткових знаків залежить від одиниці виміру. Для визначення точності обчислень користуються поняттям числа значущих цифр результату. При цьому для цілих чисел нулі справа в одних випадках – значущі цифри, а в інших випадках – ні. Число 835000 з точністю до одиниць має всі нулі значущі, але з точністю до сотень – лише один!

Наближене число містить п вірних цифр у вузькому сенсі (значенні, смислі), якщо абсолютна погрішність цього числа не перевершує половини одиниці десяткового розряду, вираженого п- ю значущою цифрою, рахуючи зліва на право, тобто, якщо виконується нерівність

Точне число А=17,976 відносно наближеного а=17,98 являється наближеним з 4-ма вірними знаками у вузькому сенсі, тому що

Наближене число містить п вірних значущих цифр в широкому сенсі, якщо абсолютна погрішність цього числа не перевищує одиниці десяткового розряду, вираженою п-ю значущою цифрою, рахуючи зліва направо, тобто, якщо виконується нерівність

Точне А=17,976 відносно а=17,97 являється наближеним а з чотирма вірними цифрами в широкому сенсі, тому що

Висновок:

Визначаючим точність обчислення є не число десяткових знаків, а число значущих цифр результату!!

2.4. Округлення чисел

Щоб погрішність була мінімальною, необхідно дотримуватись таких правил округлення:

1. Якщо перша зліва із відкинутих цифр більше 5, то остання із збережених цифр збільшується на 1. Збільшення виконується і тоді, коли перша зліва із відкинутих цифр дорівнює 5, а за нею слідують відмінні від нуля цифри.

2. Якщо перша із відкинутих цифр менше 5, то остання із збережених цифр не збільшується на 1.

3. Якщо перша зліва із відкинутих цифр дорівнює 5 і за нею не слідують відмінні від нуля цифри, то остання збережена цифра збільшується, якщо вона непарна, і не збільшується, якщо вона парна (правило парної цифри)

5,785 5,78

парна

5,775 5,78

не парна

Згідно розглянутих правил округлення абсолютна погрішність округлення не перевищує половини одиниці розряду, визначеного останньою залишеною значущою цифрою, тобто при використанні цих правил абсолютна погрішність розглядається в вузькому сенсі (значенні).

2.5. Зв’язок між числом вірних знаків та погрішністю числа

Абсолютна погрішність наближеного числа зв’язана з числом вірних значущих цифр співвідношенням 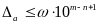, яке слідує із визначення вірної значущої цифри.

Якщо розділити це співвідношення на модуль |а|, тобто

то відносна погрішність обчислюється за формулою

,

де α₁- перша значуща цифра числа, n – кількість вірних значущих цифр, ω приймає значення 0,5 одиниці останнього розряду вірних значущих цифр у вузькому сенсі і (-1) останнього розряду вірних значущих цифр у широкому сенсі (смислі), тобто

0,5≤ ω ≤ 1.

За граничну відносну погрішність можна прийняти

Приклад 1. Яка гранична відносна погрішність наближеного числа а = 2,138 якщо це число має тільки вірні значущі цифри у вузькому сенсі?

Так як всі чотири цифри вірні у вузькому сенсі, то вибираємо ω = 0,5 і по формулі, приведеній вище, знаходимо граничну відносну погрішність

Приклад 2. Яка гранична відносна погрішність наближеного числа а = 4,735 якщо це число має тільки вірні значущі цифри у широкому сенсі?

Так як всі чотири цифри вірні у вузькому сенсі, то вибираємо ω = 1 і по формулі, приведеній вище, знаходимо граничну відносну погрішність