
- •Лекція 1. Методи наближених обчислень як розділ обчислювальної математики. Основні поняття обчислювальної математики
- •План лекції
- •1.1. Історія дисципліни «Методи обчислень»
- •1.2 Основні поняття обчислювальної математики
- •1.3. Обчислювальна задача. Чисельні методи та їх особливості
- •Коротко про головне
- •Контрольні питання
- •Лекція 2. Елементарна теорія погрішностей
- •План лекції
- •Контрольні питання
- •2.1. Точні і наближені числа. Джерела погрішностей. Класифікація погрішностей
- •2.2. Абсолютна і відносна погрішність
- •2.3. Десятковий запис наближених чисел. Значуща цифра числа.
- •2.4. Округлення чисел
- •2.5. Зв’язок між числом вірних знаків та погрішністю числа
- •2.6. Погрішність суми (різниці), добутку, частки, степені, кореня
- •2.7. Правила підрахунку вірних цифр
- •Контрольні питання
2.2. Абсолютна і відносна погрішність
Якщо a<A, то кажуть, що число а являється наближеним значенням числа А з недостачею; якщо a>A, то кажуть, що з надлишком. Різниця між точним числом А і його наближеним значенням a складає похибку, або погрішність. Якщо a>A, то a-A>0, якщо a<A, то a-A<0. Як правило, знак похибки обчислювача не цікавить, тому що він користується абсолютною погрішністю.
Абсолютна величина різниці між числом A і його наближеним значенням a називається абсолютною погрішністю наближеного числа a:
 (2.1)
(2.1)
Тут можливі два випадки:
Точне число А нам відоме. Тоді абсолютна погрішність наближеного числа знаходиться згідно з формулою (2.1).
Наприклад: нехай А=784,2737, a=784,274. Тоді абсолютна погрішність

Точне число А не відоме. Тоді обчислити абсолютну погрішність по формулі (1) неможливо. Скористаємося поняттям границі абсолютної погрішності, що задовольняє нерівність
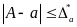
Границя абсолютної погрішності, тобто число, що заздалегідь більше, ніж абсолютна погрішність, називається граничною абсолютною погрішністю
 (2.2)
(2.2)
Значення точного числа А завжди включено в границі:

 –
з
недостачею,
–
з
недостачею,
 –
з
надлишком.
–
з
надлишком.
Значення числа А записується так:
 (2.3)
(2.3)
Приклад.
Число
54,3 отримано з округленням. Точне значення
числа невідоме. Користуючись правилами
округлення чисел, можна сказати, що
абсолютна погрішність не перевищує
0,05. Тоді границю абсолютної погрішності
можна рахувати 0,05. Записують це так
 .
Подвійний знак
означає, що відхилення наближеного
числа від точного можливе в обидві
сторони. В якості границі абсолютної
погрішності беруть якомога найменше
число.
.
Подвійний знак
означає, що відхилення наближеного
числа від точного можливе в обидві
сторони. В якості границі абсолютної
погрішності беруть якомога найменше
число.
Приклад. При вимірі довжини стрибка спортсмена виявилося, що допущена похибка не перевищує 0,5 см, тим більше вона не перевищує 1см або 2см. Кожне число можна вважати границею абсолютної погрішності. Але необхідно вибирати найменше значення, тому що воно точніше визначає наближене значення числа.
На практиці часто кажуть: “з точністю до 0,01”, “з точністю до 1см”. Це означає, що граничні абсолютні погрішності відповідно дорівнюють 0,01, 1см.
Приклад.
Якщо довжина стрибка спортсмена
 =684,1
відмірена з точністю до 0,05 см, то пишуть
=684,10,05
см. Тут гранична абсолютна погрішність
=684,1
відмірена з точністю до 0,05 см, то пишуть
=684,10,05
см. Тут гранична абсолютна погрішність
 =0,05,
а точна довжина відрізка знаходиться
в границях
=0,05,
а точна довжина відрізка знаходиться
в границях
 см.
см.
По абсолютній і граничній абсолютній погрішності не можна судити про те, добре чи погано проведено вимір!!
Приклад.
Виконано вимір шнура

 см
і аркуша паперу
см
і аркуша паперу

 см. В обох випадках гранична абсолютна
погрішність складає 0,1 см, але
визначено точніше ніж
см. В обох випадках гранична абсолютна
погрішність складає 0,1 см, але
визначено точніше ніж
 .
.
Для визначення якості проведених вимірів необхідно визначити, яку долю складає абсолютна або гранична абсолютна погрішність від виміру. В зв’язку з цим вводиться поняття відносної погрішності.
Відносною
погрішністю
 наближеного числа а
називається відношення абсолютної
погрішності
наближеного числа а
називається відношення абсолютної
погрішності
 до модуля точного числа.
до модуля точного числа.
 (2.4)
(2.4)
звідси
 (2.5)
(2.5)
Число
 ,
яке заздалегідь буде більше відносної
погрішності, називають граничною
відносною погрішністю.
,
яке заздалегідь буде більше відносної
погрішності, називають граничною
відносною погрішністю.
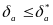 (2.6)
(2.6)
із співвідношень (2.4) та (2.6) випливає, що
 або
або

із визначення граничної абсолютної погрішності слідує, що

Тоді можна записати
 (2.7)
(2.7)
Гранична відносна погрішність буде
 (2.8)
(2.8)
Враховуючи, що А в більшості невідоме і що А ≈ а, формули (2.7) та (2.8) можна записати

 (2.9)
(2.9)
 (2.10)
(2.10)
В останньому прикладі граничні відносні погрішності будуть
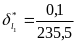 ≈0,0002460,025%
≈0,0002460,025%
 ≈0,0046510,47%
≈0,0046510,47%
Результати показують, що вимір довжини шнура був більш точний, ніж аркуша паперу.
Визначити у відсотках граничну відносну погрішність наближеного числа а=35,145+0,00074 (по (7))

