§4 Статистическое определение вероятности
Классическое определение вероятности события предполагает, что 1)число элементарных исходов конечно; 2) эти исходы равновозможны.
Однако на практике встречаются испытания с бесконечным числом различных возможных исходов. Кроме того, нет общих методов позволяющих результат испытания, даже с конечным числом исходов, представить в виде суммы равновозможных элементарных исходов.
Поэтому применение классического определения вероятности весьма ограниченно.
Мы укажем сейчас другое определение вероятности, иногда более удобное для приложений.
Пусть производится однотипных испытаний, одним из исходов которых является событие .
Определение
1. Отношение числа событий появлений
события
к общему числу испытаний n
называется относительной частотой
(частностью) события
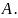
Таким
образом, обозначая через
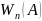относительную
частоту события
при n
испытаниях, будем иметь
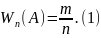
Очевидно,
.
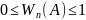Из формулы (1) получаем
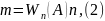
т.е. число появлений события равно его относительной частоте, умноженной на число испытаний.
При
однотипных массовых испытаниях во
многих случаях наблюдается устойчивость
относительной частоты события, т.е. при
числе испытаний
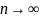относительная частота
события
колеблется около некоторого постоянного
числа p,
причем эти отклонения тем меньше, чем
больше произведено испытаний, если не
учитывать отдельные неудачные события
в статистическом смысле.
Определение 2. Под вероятностью события в статистическом смысле понимается почти достоверный предел его относительной частоты при неограниченно растущем числе испытаний.
Таким образом, почти достоверно известно, что относительная частота события приближенно совпадает с его статистической вероятностью, если число испытаний достаточно велико.
С этой точки зрения величина
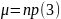
представляет собой среднее значение числа появления события при испытаниях.
При широких предположениях доказывается, что вероятности события в классическом и статистическом смысле совпадают между собой.
Пример.
В
результате ряда испытаний было обнаружено,
что при 200 выстрелах стрелок попадает
в цель в среднем 190 раз. Какова вероятность
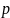поражения цели этим стрелком? Сколько
для него попаданий в цель можно ожидать
при 1000 выстрелов?
Используя статистическое определение вероятности, имеем
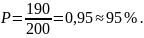
Отсюда число удачных выстрелов из 1000 выстрелов примерно составляет
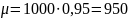
§5. Теорема сложения вероятностей
ТЕОРЕМА.
Вероятность суммы двух несовместных
событий равна сумме этих событий, т.е.
если
,
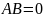то
.
(1)
Доказательство.
Пусть
из общего числа n
всех возможных и равновозможных
элементарных исходов испытания
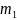благоприятствуют событию
,
а
-
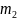событию
.
Так как события
и
несовместны, то появление события А
исключает появление события В и обратно;
поэтому число благоприятных исходов
события
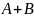в точности равно
.
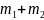Отсюда на основании классического
определения вероятности получаем
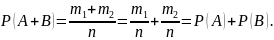
Следствие. Вероятность суммы конечного числа попарно несовместных событий равна сумме вероятностей этих событий.
Пусть,
например, события
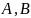и
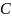попарно несовместны, т.е. события
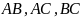невозможны.
Имеем
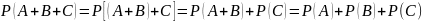
Замечание. Пусть события А и B совместны. Тогда число благоприятных элементарных исходов для события A+B будет
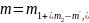
где
-
число элементарных исходов, благоприятных
для события
.
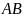Действительно, складывая числа исходов
и
,
благоприятных событиям
,
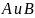мы исходы, благоприятные событию
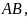считаем два раза; следовательно, при
подсчете числа исходов для события
излишнее значение m’
следует отбросить.
Поэтому, в общем случае имеем
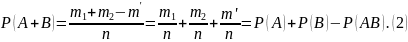
Следствие.
Так как
,
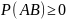то из формулы (2) имеем
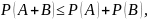(3)
т.е. вероятность суммы двух событий никогда не превосходит суммы вероятностей этих событий.
Это утверждение, очевидно справедливо также и для нескольких событий.
Пример. В урне находятся 2 белых, 3 красных и 5 синих одинаковых по размеру шаров. Какова вероятность того, что шар случайным образом извлеченный из урны, будет цветным (не белым)?
Пусть
событие
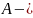извлечение
красного шара из урны, а событие
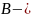извлечение синего шара. Тогда событие
есть извлечение цветного шара из урны.
Очевидно, имеем
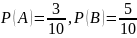
Так как события и несовместны (извлекается только один шар), то по теореме сложения имеем
