ЭЛЕКТРОННОЕ УЧЕБНОЕ ПОСОБИЕ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ

УГНТУ

Стерлитамак

Биккулов.И.М

ОГЛАВЛЕНИЕ

Основные определения и теоремы

Случайные события………………………………………………………...3

Алгебра событий…………………………………………………………...5

Классическое определение вероятности………………………………….7

Статистическое определение вероятности……………………………...11

Теорема сложения вероятностей………………………………………...13

Полная группа событий…………………………………………………..15

Теорема умножения вероятностей………………………………………16

Формула полной вероятности……………………………………………20

Повторные независимые испытания

Элементы комбинаторики………………………………………………..23

Биномиальный закон распределения вероятностей…………………….26

Локальная теорема Лапласа.……………………………………………..28

Интегральная теорема Лапласа…………………………………………..30

Теорема Пуассона…………………………………………………………34

Случайная величина и её числовые характеристики

Случайная дискретная величина и её закон распределения…………...36

Математическое ожидание……………………………………………….39

Основные свойства математического ожидания………………………..40

Дисперсия………………………………………………………………….45

Непрерывные случайные величины. Функция распределения………...51

Числовые характеристики непрерывной случайной величины………..55

Равномерное распределение……………………………………….……..56

Нормальное распределение……………………………………….……...58

Упражнения………………………………………………………….……62

Мода и медиана…………………………………………………….……..64

Показательное (экспоненциальное) распределение. Функция надежности……………………………………………………………………….66

Система случайных величин……………………………………………..70

Приложение

Литература

Основы теории вероятностей а. Основные определения и теоремы

§1. Случайные события

В естественных науках познание действительности происходит в результате испытаний (экспериментов) или наблюдений, т. е опыта в широком понимании слова. Под испытанием (наблюдением), в общем смысле, подразумевается наличие определенного комплекса условий. Возможный результат - исход испытания или наблюдения - называется событием, независимо от его значимости.

При построении теории события идеализируются, т. е игнорируются ситуации для данного явления.

Пример. При бросании монеты может выпасть герб или решетка (обратная сторона). Таким образом, при однократном испытании возможны два события: А – выпадение герба, В – выпадение решетки.

Однако возможно еще одно событие 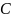– когда монета станет на ребро. Но при организации игры в «орлянку» это обстоятельство несущественно ( монета перебрасывается!) и в нашем идеализированном опыте не учитывается.

Определение 1. Результат испытания, который нельзя заранее прогнозировать, называется случайным событием.

Иными словами, событие является случайным в данном опыте, если нельзя заранее предсказать, произойдет оно или не произойдет в этом опыте.

Например, случайным событием является выпадение герба при бросании монеты. Конечно, предполагается, что испытание организовано так, что исход его заранее не известен.

Во многих случаях случайное событие есть результат неполной информации о данном явлении. Например, в опыте с бросанием монеты, если нам были бы известны сила толчка, форма монеты, закон сопротивления воздуха и другие факторы, определяющие закон движения монеты, мы смогли бы точно предсказать исход события.

Определение 2. Событие называется достоверным в данном испытании (т. е при осуществлении определенной совокупности условий), если оно неизбежно происходит при этом испытании.

Например, получение студентом положительной или отрицательной оценки на экзамене есть событие достоверное, если экзамен протекает согласно обычным правилам.

Определение 3. Событие называется невозможным в данном испытании, если оно заведомо не происходит в этом испытании.

Например, если в урне находятся лишь цветные (небелые) шары, то извлеченные из этой урны белого шара есть событие невозможное. Отметим, что при других условиях опыта появление белого шара не исключается; таким образом, это событие невозможно лишь в условиях нашего опыта.

Теория вероятностей есть наука, изучающая закономерности случайных событий.

В связи с развитием новой техники особый интерес представляют статистические закономерности массовых однородных случайных событий (контроль качества продукции, обслуживание серийного производства, работа телефонной станции и т. п). Здесь в различных вариантах установлена основная теорема теории вероятностей – закон больших чисел.

Примем как аксиому, что для каждого события А можно определить, по крайней мере, теоретически, вероятность этого события – число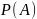 , представляющее, в некотором смысле, «меру достоверности» данного события и подчиненное естественным требованиям. Предполагается, что вероятность любого события удовлетворяют неравенству

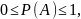
причем вероятность невозможного события равна нулю, а вероятность достоверного события равна единице.

На практике считают, что если вероятность события мала, то это событие практически невозможно; наоборот, если вероятность события равна единице, то это событие почти достоверно; и сообразно этому принимают обоснованные решения.

В создании теории вероятностей участвовали многие крупные математики (Паскаль, Ферма, Лапласс, Гаусс, Пуассон и др.). В более поздний период решающие успехи принадлежат отечественным математикам (Чебышев, Марков, Бернштейн, Колмогоров, Хинчин и др.).

Теория вероятностей широко используется в теоретических и прикладных науках (в физике, геодезии, в теории стрельбы, в теории автоматического управления и многих других). В частности, она служит теоретической базой математической и прикладной статистики, на основе которых происходит планирование и организация производства.