Лекція 7

Розпізнавання з навчанням.

Методи навчання використовують для побудови систем розпізнання при відсутності повної початкової інформації, об’єм якої дозволяє розділити об’єкти на класи на мові апріорного словника ознак . Такими описами можуть бути:

• розділяючи функції ;

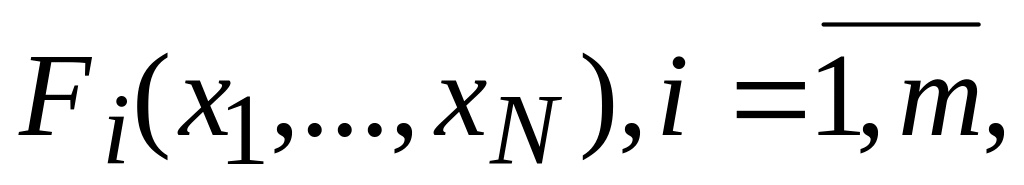• апріорні імовірності появи об’єктів різних класів;

• умовні густини розподілів .

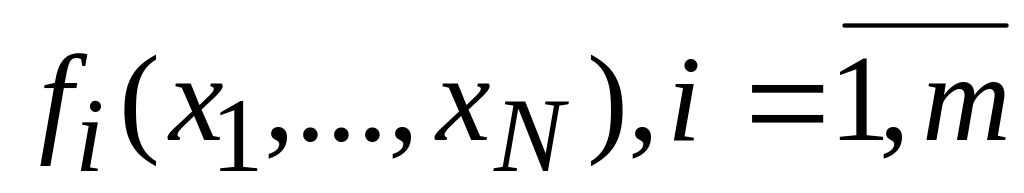7.1. Суть процедури навчання.

Нехай початкова інформація дозволяє скласти список об’єктів з зазначенням класів , до яких вони відносяться, тобто:

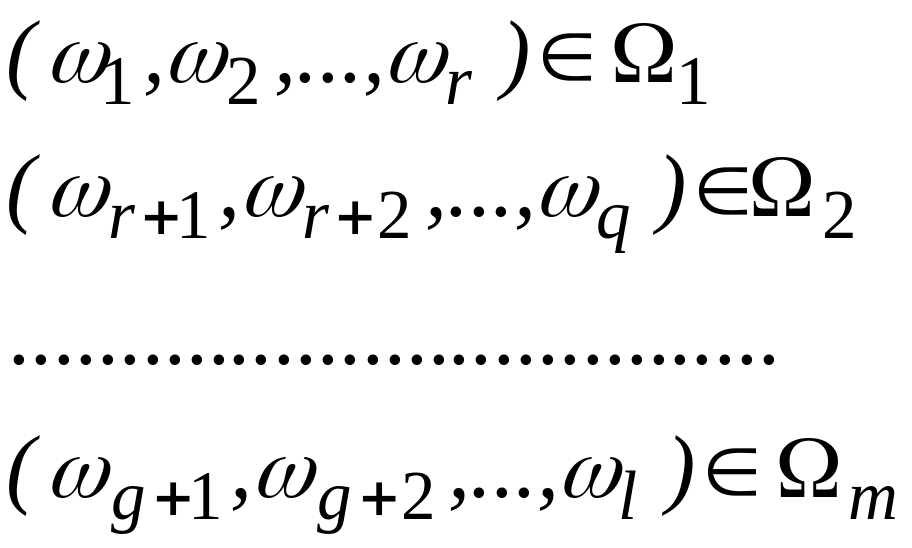
Оскільки апріорний ознаковий простір визначений, то кожний об’єкт може бути описаний на мові ознак . Отже, ознаки об’єкта:

і т.д.

Таким чином, початковий список може бути представлений у виді навчальної послідовності:

.

Таким чином, навчальна вибірка дозволяє на основі різних методів і алгоритмів реалізувати процедуру навчання. Проте така ситуація не є достатньою для отримання необхідної точності і тому необхідно використовувати апріорну інформацію. Якщо навчальна є достатньо репрезентативна, тобто об’єкти більш-менш рівномірно розподілені по областях простору ознак, які відповідають конкретним класам, то в границі подібна процедура приводить до достатньо точного опису класів.

7.2. Постановка задачі

Нехай вся множина об’єктів розбита на класи , визначено вектор ознак , які складають апріорний словник ознак; визначена вибірка фіксованої довжини, тобто об’єкти ; вектори, якими вони описуються ; встановлена відповідність між об’єктами і вагами; задані апріорні імовірності і умовні густини .

Необхідно на основі цієї вибірки пред’явленої системи і цих даних побудувати у просторі ознак гіперповерхню, яка розділяє цей простір на області , які відповідають класам . І таке розділення необхідно здійснити найкращим в даному тому чи іншому сенсі чином.

Скористуємось методом дихотомії.

Обмежимось двома класами і . До дихотомії можна послідвно звести і загальний випадок, коли число класів m>2.

Позначимо розділяючу функцію

, (1)

- невідомий вектор параметрів.

Знаки розділяючої функції визначають області D₁ і D₂ в N-мірному просторі ознак, які відповідають класам і :

(2)

Навчальна вибірка вказує належність об’єктів до класу або

(3)

Умова (3) використовується для визначення двох систем нерівностей, тобто, якщо з допомогою розділяючої функції об’єкт класифікується правильно, то >0, а якщо помилково, то <0.

Мірою відхилення від y вибирають деяку випуклу функцію від різниці y і , тобто:

(4)

Пред’явлення об’єктів здійснюється випадковим чином, внаслідок чого і міра відхилення також є випадковою.

За міру, яка найкращим чином характеризує, наскільки добре вибрана розділяюча функція, доцільно вибрати функціонал:

(5)

де - математичне сподівання.

Найкращий вибір розділяючої функції буде зроблено тоді, коли досягає мінімуму. Таким чином, задача зводиться до визначення вектора , який забезпечує:

(6)

При цьому обмежуючою умовою для отримання оптимального рішення є вид розділяючої функції.

Оскільки невідома густина розподілу , то невідоме і . Тому визначення вектора реалізується в два етапи.

1.Значення визначається наближено на основі апріорної інформації, яка міститься в навчальній послідовності, в результаті знаходять значення .

2.Для уточнення значення і отримання значення , яке мінімізує функціонал (5), використовується апостеріорна інформація.

Реалізація цих етапів може здійснюватись однаковими алгоритмами, але розділ на два етапи має принципове значення.