Лекція 6 Розпізнавання без навчання.

По відношенню до об’єму апріорної вхідної інформації системи розпізнавання поділяють на:

• системи розпізнавання без навчання;

• системи розпізнавання з навчанням;

• системи розпізнавання з самонавчанням.

Системи розпізнавання без навчання.

Для таких систем наявним є повна початкова апріорна інформація, що складає:

• відомості про суть і природу об’єктів та явищ; які рішення будуть прийматися (на основі цих даних вибираються принцип і проводиться класифікація).

• дані, що забезпечують побудову апріорного словника ознак та обмежень на створення вимірювальної апаратури системи;

• дані для визначення залежності між класами об’єктів і ознаками апріорного словника 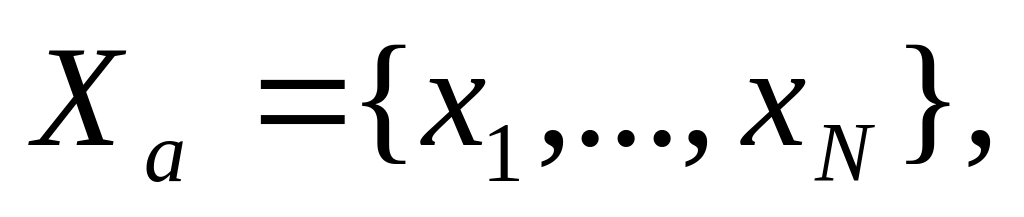якими вони характеризуються.

Опис класів мовою ознак після складання алгоритму розпізнавання, який базується на відповідній мірі близькості, дозволяє розв’язати задачу побудови робочого словника ознак системи розпізнавання, а потім знову вернутися до задачі опису класів, але вже на мові ознак робочого словника .

Якщо ознаки імовірнісні, то описами класів є умовні густини розподілу імовірностей значень ознак x₁,…,x_N для кожного класу , тобто функції , а також апріорні ймовірності появи об’єктів відповідних класів.

При побудові функцій розрізняють дві ситуації.

1. Аналітичний вид функції відомий і треба визначити значення параметрів (параметрична оцінка).

2. Аналітичний вид невідомий. Необхідно оцінити і вид функції і її параметри (непараметрична оцінка).

6.1 Параметричне оцінювання.

Параметричне оцінювання має місце в досить простих ситуаціях і виконується різними методами.

1.Метод максимуму правдоподібності Фішера. Нехай Х – m-вимірна випадкова величина, задана функцією густини виду , де -невідомий параметр або вектор параметрів, і вибіркою незалежних реалізацій об’ємом N. Ця вибірка належить до системи N незалежних однакових m-вимірних випадкових величин . Загальна мірність системи mN.

Реалізацію, яка складає цю вибірку можна представити у вигляді вектора довжиною N, кожна з компонента з компонент якого є m-мірна величина де .

Значення сумісної функції густини такої системи випадкових величин в т. рівне і називається функцією правдоподібності (функцією параметра ).

Значення , при якому ця функція досягає максимуму, називається оцінкою максимальної правдоподібності параметра  (ОМП). ОМП визначають, максимізуючи користуючись тим, що ln x- є строго зростаюча функція.

Шукане значення  знаходять з рівняння

.

2.Метод Байєса. В цьому методі параметр  вважають випадковою величиною з відомою апріорною густиною f(). Апостеріорні імовірнісі ваги  розраховуються по вибірці , отриманій у відповідності с густиною f(x).

Оцінка функції густини визначається як неперервна суміш густин з апостеріорними імовірнісними вагами

,

де - область можливих значень . Апостеріорна функція густини  визначається за правилом Байєса:

.

Якщо вид функції густини заданий гіпотетично, то оцінка функції густини не завершується вибором її параметрів. Необхідна перевірка гіпотези про вид функції густини емпіричної інформації. Найбільш поширена перевірка гіпотези критерієм Пірсона, який не залежить ні від виду ні від мірності функції.

За міру відхилення емпіричної функції від гіпотетичної (передбачуваної, можливої, припустимої) розглядається величина

,

де N – кількість реалізацій у вибірці,

n – кількість інтервалів гістограми,

- частота попадання реалізації в і-й інтервал в N реалізаціях;

- імовірність попадання в і-й інтервал, вичислена по гіпотетичній функції густини.