
Інтеграл та первісна
Обчисліть інтеграл
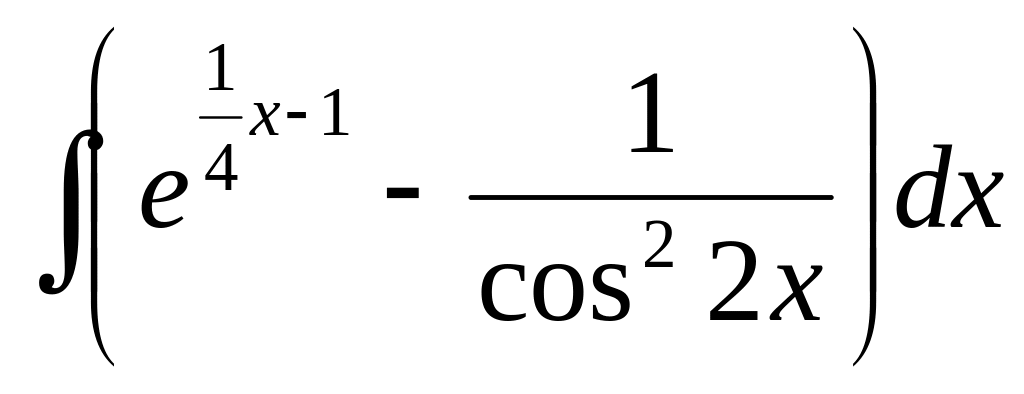
Обчисліть інтеграл

Обчисліть інтеграл

Обчисліть інтеграл

Обчисліть інтеграл

Обчисліть інтеграл

Обчисліть інтеграл

Обчисліть інтеграл

Обчисліть інтеграл

Обчисліть інтеграл

Обчисліть інтеграл

Обчисліть інтеграл
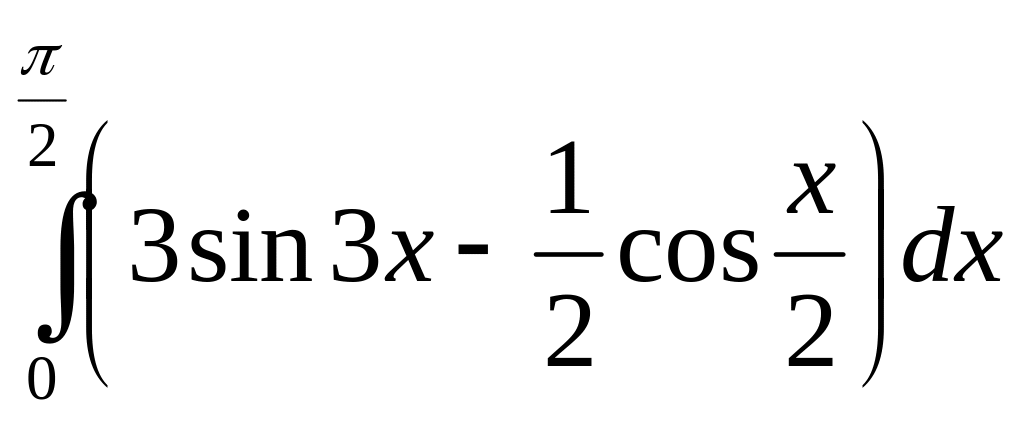
Обчисліть
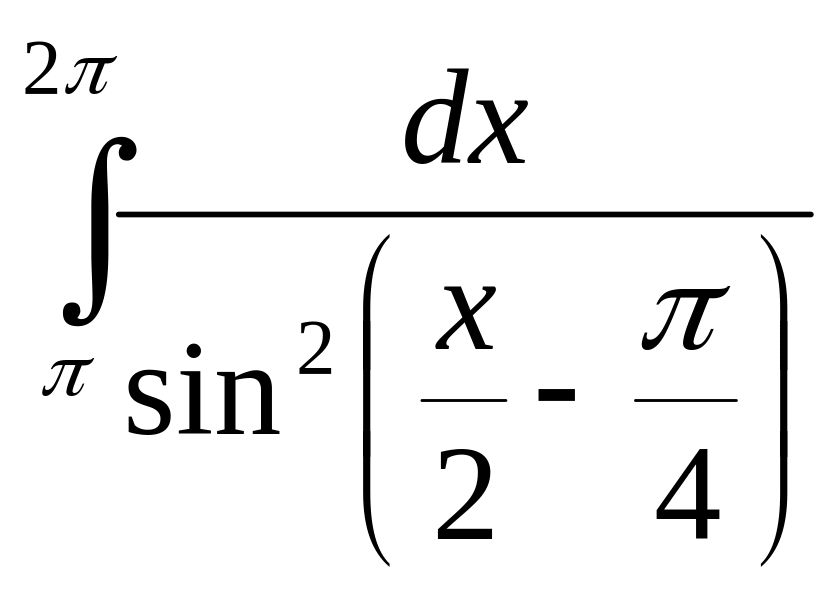
Обчисліть інтеграл
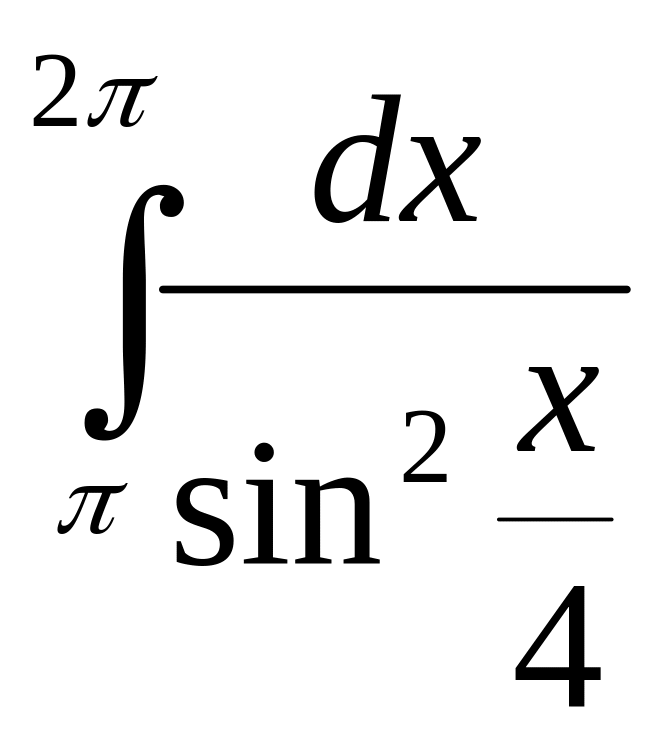

Обчисліть інтеграл

Обчисліть інтеграл


Обчисліть інтеграл

Знайдіть первісну функції
 ,
графік якої проходить через точку В
(-1; 12)
,
графік якої проходить через точку В
(-1; 12)Знайдіть первісну функції
 ,
графік якої проходить через точку М
(-2; 10)
,
графік якої проходить через точку М
(-2; 10)Знайдіть первісну функції
 графік
якої проходить через точку
графік
якої проходить через точку
Знайдіть первісну функції
 графік
якої проходить через точку
графік
якої проходить через точку
Знайдіть первісну функції
 графік
якої проходить через точку
графік
якої проходить через точку
Знайдіть первісну функції
 графік
якої проходить через точку
графік
якої проходить через точку
Знайдіть первісну функції
 ,
графік якої проходить через точку А
(9; 30)
,
графік якої проходить через точку А
(9; 30)Знайдіть первісну функції
 ,
графік якої проходить через точку А
(4; 5)
,
графік якої проходить через точку А
(4; 5)Знайдіть первісну функції
 ,
графік якої проходить через початок
координат
,
графік якої проходить через початок
координатЗнайдіть первісну функції
 ,
графік якої проходить через точку А
(1; 4)
,
графік якої проходить через точку А
(1; 4)Знайдіть первісну функції
 ,
графік якої проходить через точку А
(π; 3)
,
графік якої проходить через точку А
(π; 3)Знайдіть первісну функції
 ,
графік якої проходить через точку
,
графік якої проходить через точку
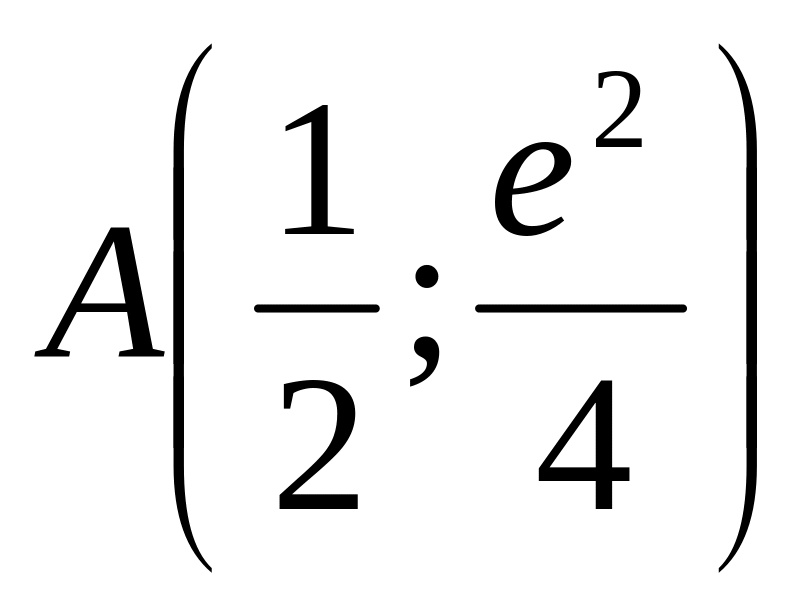
Знайдіть первісну функції
 ,
графік якої проходить через точку А
(1; 3е)
,
графік якої проходить через точку А
(1; 3е)
Для функції
 знайдіть таку первісну
знайдіть таку первісну
 що
що

Для функції
 знайдіть первісну, графік якої проходить
через точку
знайдіть первісну, графік якої проходить
через точку

Знайдіть площу фігури, обмеженої лініями
 і х=1
і х=1Знайдіть площу фігури, обмеженої лініями
 і
і

Знайдіть площу фігури, обмеженої лініями


Знайдіть площу фігури, обмеженої лініями

Обчисліть площу трикутника, утвореного осями координат і дотичною графіка функції
 в точці з абсцисою х0=3
в точці з абсцисою х0=3Обчисліть площу фігури, обмеженої параболою
 і прямою
і прямою

Обчисліть площу фігури, обмеженої параболою
 і прямою
і прямою

Обчисліть площу фігури, обмеженої параболою
 і прямою
і прямою

Знайдіть площу фігури, обмеженої лініями

Обчисліть площу фігури, обмеженої параболою
 і прямою
і прямою

Обчисліть площу фігури, обмеженої параболою
 і прямою
і прямою

Обчисліть площу фігури, обмеженої гіперболою
 і прямою х+у=8
і прямою х+у=8Обчисліть площу фігури, обмеженої гіперболою
 і прямою
і прямою

Обчисліть площу фігури, обмеженої гіперболою
 та прямими у=4
і х=4
та прямими у=4
і х=4Швидкість руху точки задається рівнянням

 Знайдіть
рівняння руху
Знайдіть
рівняння руху
 ,
якщо
,
якщо

Планіметрія
Висота АМ трикутника АВС ділить його сторону ВС на відрізки ВМ і МС. Знайдіть довжину відрізка МС, якщо АВ=10√2 см, АС=26 см, <В=45.
Висота BD трикутника АВС ділить його сторону AС на відрізки AD і СD. Знайдіть довжину відрізка СD, якщо АВ=2√3 см, BС=5 см, <A=60.
Відрізок AD –бісектриса трикутника ABC, AD=l , <C=90, <BAC=α Знайдіть довжину відрізка BD
У трикутника
 відрізок AD
– бісектриса . Знайдіть довжину відрізка
AD
відрізок AD
– бісектриса . Знайдіть довжину відрізка
ADКатет прямокутного трикутника дорівнює 6 см, а медіана, проведена до нього,- 5см. Знайдіть гіпотенузу трикутника.
Катети прямокутного трикутника дорівнює 6 см і 8 см. Знайдіть відстань від вершини меншого гострого кута трикутника до центра вписаного кола
Катет прямокутного трикутника дорівнюють 18 см і 24 см. Знайдіть бісектрису трикутника, проведену з вершини меншого гострого кута.
Довжини сторін трикутника дорівнюють відповідно 11см, 12 см і 13 см. Знайдіть довжину медіани, яка проведена до більшої сторони.
У трикутник АВС вписано ромб АКРЕ так, що кут А у них спільний, а вершина Р належить стороні ВС. Знайдіть сторону ромба, якщо АВ=6см, АС=3см.
Висоти паралелограма дорівнюють 8 см і 12 см, а кут між ними - 60. Знайдіть площу паралелограма.
Бісектриса тупого кута паралелограма ділить його сторону на відрізки завдовжки 3 см і 5 см, рахуючи від вершини гострого кута. Обчисліть площу паралелограма, якщо його гострий кут дорівнює 60°
Бісектриса кута прямокутника ділить його діагональ у відношенні 2:7. Знайдіть площу прямокутника, якщо його периметр дорівнює 108 см.
Площа ромба дорівнює 120 см2, а його діагоналі відносяться як 5:12. Знайдіть периметр ромба.
Один з катетів прямокутного трикутника дорівнює 30 см, а радіус описаного навколо нього кола – 17 см. Обчисліть площу даного трикутника.
Знайдіть площу круга, вписаного в трикутник зі сторонами 4см, 13 см і 15 см.
Менша основа прямокутної трапеції дорівнює 12 см, а менша бічна сторона - 4√3 см. Знайдіть площу трапеції, якщо один з її кутів дорівнює 120°
Основи рівнобічної трапеції 9 і 21 см, а висота – 8 см. Знайдіть радіус кола, описаного навколо даної трапеції.
У рівнобічної трапеції ABCD основа ВС дорівнює 6 см, висота трапеції дорівнює 2√3см, а бічна сторона утворює з основою AD кут 60°. Знайдіть основу AD трапеції.
