9 Класс

1. При изготовлении льда в комнатном холодильнике потребовалось 5 мин, чтобы охладить воду от +4˚С до 0˚С, и еще 1 час 40 мин, чтобы превратить ее в лед. Определите удельную теплоту плавления льда. Удельная теплоемкость воды 4,210³ Дж/кг˚С.

Возможное решение.

Количество теплоты, отводимое от холодильной камеры в единицу времени, равно q. Тогда за время t количество отведенной теплоты равно Q=qt. Для охлаждения некоторой массы m воды требуется отвести от него количество теплоты Q₁=cmt, где c – удельная теплоемкость воды, t – разность между начальной и конечной температурами воды. Так как на охлаждение воды до нуля градусов потребовалось время t₁=5 мин, то, приравняв Q и Q₁, получим .

Для кристаллизации льда необходимо отвести от него количество теплоты Q₂=m, где  - удельная теплота плавления льда. Это количество теплоты отводится холодильником за время t₂=100 мин. Поэтому . Подставляя в это уравнение q, получим

Примерные критерии оценивания.

Указана пропорциональность количества теплоты от времени при постоянной производительности холодильника…………………………1

Записана формула для количества теплоты, которое требуется отвести для охлаждения некоторой массы m воды……………………………..0,5

Записана формула для количества теплоты, которое требуется отвести для кристаллизации льда………………… ……………………………..0,5

Составлена система уравнений………………………………………….1

Решена система уравнений……………………………………………….1

Произведен правильный расчет………………………………………….1

2. В сосуде находится некоторое количество воды, в которой плавает пробка. На сколько процентов изменится объем надводной части пробки, если из колбы выкачать воздух? Плотностью образовавшихся после откачки паров воды можно пренебречь. Плотность воды равна 1 г/ см³, воздуха 1,3 кг/ м³.

Возможное решение.

П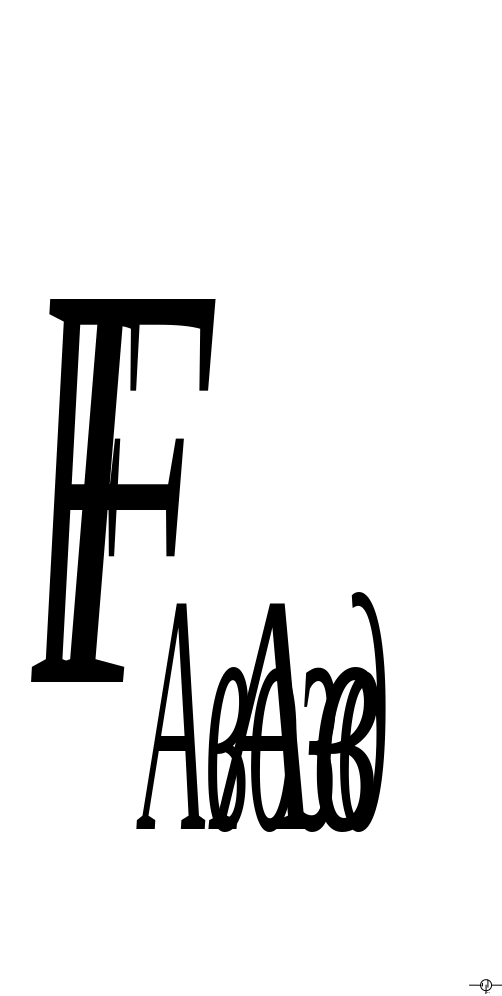 усть V₀ – объем сосуда, V₁ и V₂ – объемы надводных частей пробки в воде до и после откачки воздуха, _п, _в, _возд – плотности пробки, воды и воздуха соответственно. Из условия равновесия пробки до откачки имеем: mg + F_{A возд} + F_{A в} = 0, где F_{A возд}, F_{A в}  выталкивающие силы, действующие на пробку со стороны воздуха и со стороны воды. Эти силы направлены в разные стороны, как показано на рисунке. Аналогично, после откачки: mg + F_{A в 1} = 0. Учитывая, что m= _п V₀, F_{A возд} = _воздg V₁, F_{A в} = _в g(V-V₁), F_{A в 1}= _в g(V-V₂), получаем

_п V₀ g + _воздg V₁ + _в g(V-V₁)=0 и _п V₀ g + _в g(V-V₂)=0. Решая систему полученных уравнений, имеем:

Примерные критерии оценивания.

Определены силы, действующие на пробку………………………………1

Записано условия равновесия пробки до откачки воздуха……………….1

Записано условия равновесия пробки после откачки воздуха…………0,5

Записана формула для определения массы пробки……………………..0,5

Записана формула для расчета силы Архимеда со стороны воды до откачки воздуха ….……………………………………………………………1

Записана формула для расчета силы Архимеда со стороны воды после откачки воздуха.….…………………………………………………………1

Записана формула для расчета силы Архимеда со стороны воздуха……1

Решена система полученных уравнений…………………………………..1

Произведен расчет…………………………………………………………..1

3. В цилиндрических сообщающихся сосудах находится ртуть. Площадь поперечного сечения широкого сосуда в 5 раз больше площади поперечного сечения узкого сосуда. В узкий сосуд наливают воду, которая образует столб высотой 34 см. На сколько поднимется уровень ртути в широком сосуде и на сколько опустится в узком?

Возможное решение

Пусть относительно начального уровня ртути в сосудах в узком сосуде уровень ртути понизится на h₂, а в широком повысится на h₁. Тогда давление столба воды высотой H в узкой трубке будет равно gρ_вH, давление воды в широкой трубке равно gρ_р(h₁+h₂), где  _k - плотность керосина и  _в – плотность воды Так как жидкости находятся в равновесии, то gρ_вH = gρ_р(h₁+h₂). Ртуть можно считать несжимаемой жидкостью, поэтому уменьшение объема в узкой трубке площадью S должно быть равно увеличению объема в широкой трубке площадью 5S: S h₂ = 5S h₁, или h₂ = 5h₁. Подставив найденное значение h₂ в первую формулу, найдем

. Вычисления дают h₁ = 0,4 см; h₂ = 2 см.

Примерные критерии оценивания.

Записано условие равновесия жидкости в сообщающихся сосудах…1

Выражено давление воды в узком сосуде…………………………...0,5

Выражено давление ртути в широком сосуде…………………………1

Найдено соотношение между h₂ и h₁…………………………………..1

Записано выражение для h₂ и h₁………………………………...……..1

Произведен расчет h₂ и h₁………………………………...………….0,5

3. Трехламповую люстру с двумя выключателями подключили к сети. При проверке оказалось, что допущены ошибки, в результате которых: 1) при включении первого выключателя загорается только одна лампочка; 2) при включении только второго выключателя горят все три лампочки, но не полным накалом; 3) при одновременном включении двух выключателей снова горит только одна лампа. Нарисуйте возможную схему ошибочного подключения, объясните наблюдаемые эффекты.

Возможное решение.

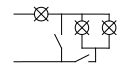
Примерные критерии оценивания.

Предложен один вариант схемы………………………………………..2

Предложено два варианта схемы…………………………………..…..4

Объяснены наблюдаемые эффекты…………………………………….1

3. Какой жидкостный барометр более точный – наполненный ртутью, водой или спиртом? Почему?

Возможное решение.

Высота столба жидкости в барометре зависит от плотности этой жидкости при данном атмосферном давлении обратно-пропорционально, т. е.

Следовательно, наибольшая высота столба будет у спирта, так как его плотность самая маленькая.

Примерные критерии оценивания.

Записано равенство давлений столба жидкости в барометре и атмосферного давления……………………………………………………..1

Записана формула давления столба жидкости……………………….1

Найдена зависимость высоты столба жидкости от плотности………1

Проведен анализ данной зависимости…………………………….......1

Дан правильный ответ на вопрос задачи………………………………1