1.11.1 Нахождение пути, пройденного телом при прямолинейном движении.

Как известно, путь, пройденный телом при равномерном движении за время t, вычисляется по формуле S=v t.

Если тело движется неравномерно в одном направлении и скорость его меняется в зависимости от времени, т.е. v=f(t),то для нахождения пути, пройденного телом за время от t=a до t=b, можно воспользоваться формулой

Пример 21

Найти путь, пройденный телом за три секунды и за третью секунду движения, если его скорость задается формулой v(t)=e^2х м/с.

Решение:

1). Путь, пройденный за три секунды:

2).Путь, пройденный за третью секунду:

Ответ: 1) за три секунды тело пройдёт путь 201,121(м);

2) за третью секунду тело пройдёт путь 198,02 (м)

1.11.2 Нахождение работы переменной силы.

Пусть под действием переменной силы F(x) тело перемещается из точки х=а в точку х=b. Тогда работа силы F(x) по перемещению тела находится по формуле:

Пример 22

Силой в 40 Н пружина растягивается на 8 см. Первоначальная длина пружины равна 10 см. Какую работу надо совершить, чтобы растянуть пружину до 15 см?

Решение:

При растяжении пружины сила воздействия F(x) численно равнa силе упругости Fупр=kx, где k- жесткость пружины, х- абсолютное удлинение. Найдем жесткость пружины:

k=F(x)/x= 40H/0,08м= 500 Н/м

Тогда F(x) = 500x, пружину необходимо растянуть на 15-10=5см=0,05м и тогда работа равна

Ответ: для растяжении пружины до 15 см необходимо совершить работу 0,625 (Н).

1.11.3Вычисление силы давления жидкости на вертикально расположенную

пластину.

По закону Паскаля сила давления жидкости на вертикально расположенную пластину равна силе давления жидкости на горизонтально расположенную пластину той же площади погруженную на ту же глубину. Сила давления жидкости на вертикально расположенную пластину вычисляется по формуле:

Г де у=f(x) – функция, выражающая зависимость длины поперечного сечения пластины от уровня погружения х, g- ускорение свободного падения, - плотность жидкости.

Пример 23

Определить силу давления воды на вертикальную пластинку длиной 20м и высотой 8м, верхнее основание которой находиться ниже поверхности жидкости на 2м.

Решение:

Свободная поверхность жидкости

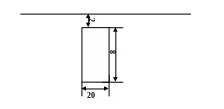
f(x) =20 , a=2, b=8+2=10, g=1000кг/м³, тогда сила давления жидкости

Р=9,81·1000·

Ответ: Сила давления жидкости на пластинку равна 9,418∙10⁶(Н).

Пример 24

Вычислить силу давления воды на треугольную пластину АВС с основанием АС=9м и высотой ВD=2м, вертикально погруженную в жидкость, если вершина В лежит на свободной поверхности жидкости, а АС параллельна ей.

Решение:

Пусть MN –поперечное сечение пластины на уровне ВЕ =х. Найдем зависимость длины MN от х .Из подобия треугольников MNB и АВС имеем:

или .

Отсюда MN=f(x)=4,5·x. Тогда

f(x) =4,5х , a=0, b=BD=2, g=1000кг/м³

В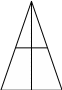

M E N

A C

D

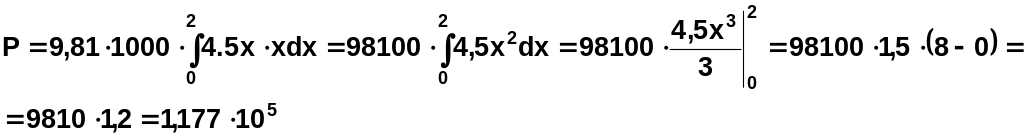
Ответ: Сила давления жидкости на пластинку равна 1,177∙10⁵(Н).

Литература:

[1] стр. 228-235, [2] стр. 302-305, [3] стр. 293-294, [4] стр. 355-363