1.2 Производные высших порядков. Физический смысл производной

Пусть материальная точка движется прямолинейно по закону S=S(t), тогда

1. Скорость прямолинейного движения материальной точки в момент времени t равно первой производной от пути по времени.

2. Ускорение прямолинейного движения материальной точки в момент времени t равно первой производной от скорости по времени или второй производной от пути по времени

Пример 2.

Тело движется прямолинейно по закону , где S – путь (м), t- время (с). Найти скорость и ускорение тела в момент времени t=1с.

Решение:

1)

(м/с)

2)

(м/с²)

Ответ: в момент времени t=1 скорость тела равна 5 м/с, а ускорение равно 3 м/с².

Литература:

[1] стр. 173-175, [2] стр. 179-180, [3] стр. 209, 218 -219, [4] стр. 237-242, [5] стр. 120-121

1.3 Геометрический смысл производной. Уравнение касательной и нормали к плоской кривой

Производная функции в точке равна угловому коэффициенту касательной, проведённой к графику функции в этой точке.

Уравнение касательной к графику функции у = f(х) в точке с абсциссой х₀ имеет вид:

Уравнение нормали к графику функции у=f(х) в точке с абсциссой х₀ имеет вид:

Алгоритм составления уравнения касательной и нормали

1. Обозначьте абсциссу точки касания х₀.

2. Вычислите f(х₀).

3. Найдите 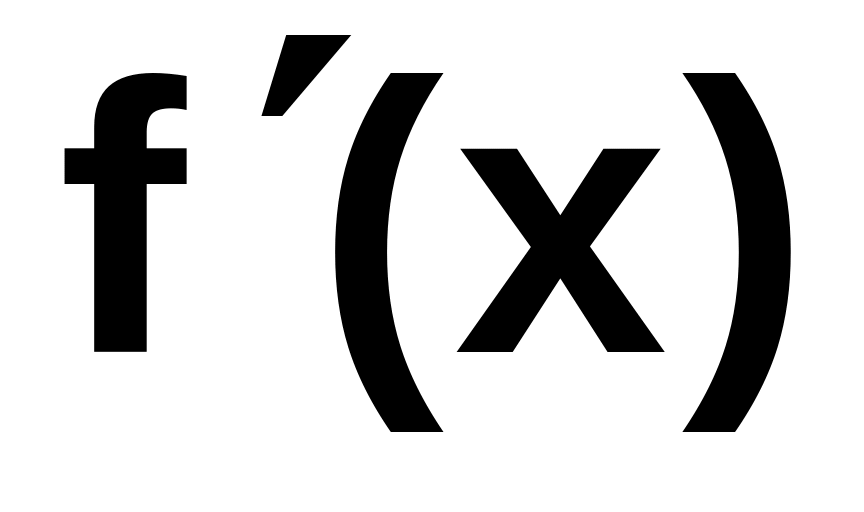и вычислите .

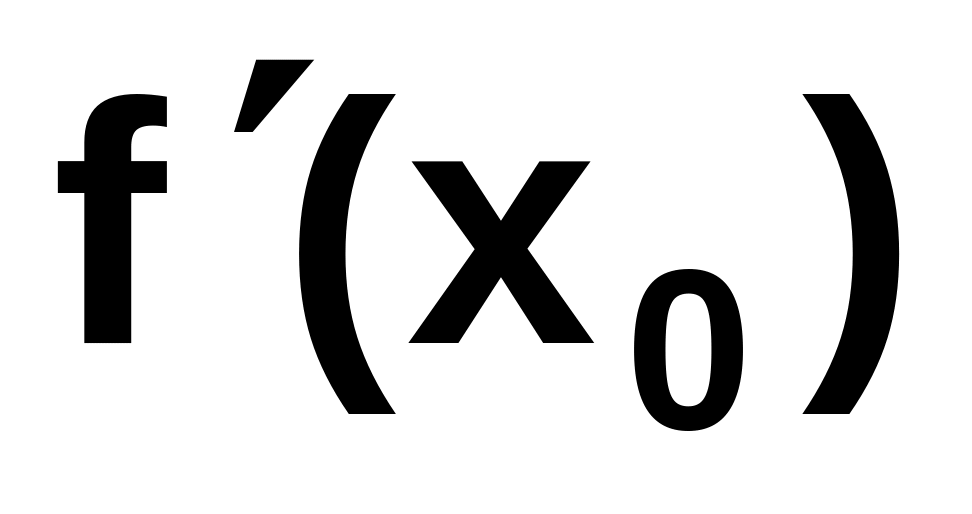4. Найденные значения х₀, f(х₀), подставьте в уравнение касательной и нормали.

5. Выполните упрощение, полученных уравнений.

Пример 3.

Составьте уравнение касательной к графику функции f(х)=х²+6х+5 в точке с абсциссой

х₀ = -2.

Решение.

1. х₀=-2

2. f(х₀)=(-2)²+6(-2)+5= -3

3. =2х+6

= =2(-2)+6=2

4. касательная: у= -3+2(х-(-2))

у= -3+2(х+2)

у= -3+2х+2

у=2х+1

5. Нормаль:

Ответ: у=2х+1 – уравнение касательной , - уравнение нормали

Литература:

[1] стр. 139-144, [2] стр. 199-201, [3] стр. 207-209, [4] стр. 231-236, [5] стр. 87-91

4. Исследование функции с помощью производной. Построение графика функции.

Справочный материал

Достаточные условия монотонности (возрастания, убывания) функции:

1. Если производная дифференцируемой функции положительна на промежутке, то функция на этом промежутке возрастает.

2. Если производная дифференцированной функции отрицательна на промежутке, то функция на этом промежутке убывает.

Необходимое и достаточные условия экстремума функции:

1. Если функция имеет экстремум в точке, то в этой точке производная либо равна нулю, либо бесконечна, либо не существует

2. Если в стационарной точке х=а производная функции меняет свой знак с плюса на минус (с возрастания на убывание), то функция в этой точке имеет максимум, если с минуса на плюс, то функция имеет минимум.

Алгоритм определения промежутков монотонности и экстремумов функции

1. Найдите область определения функции.

2. Найдите производную функции.

3. Найдите стационарные и критические точки, т. е точки в которых производная функции равна нулю или не существует.

4. Отметьте стационарные и критические точки на числовой прямой и определите знаки производной на получившихся промежутках.

5. Сделайте выводы (стрелками) о монотонности функции.

6. Сделайте выводы о точках экстремума функции.

Достаточные условия выпуклости и вогнутости графика функции:

1. Если для дважды дифференцируемой функции вторая её производная отрицательна внутри промежутка, то график функции является выпуклым на данном промежутке.

2. Если же вторая производная положительна внутри промежутка, то график функции является вогнутым на данном промежутке.

Алгоритм определения промежутков выпуклости и вогнутости графика функции

1. Найдите вторую производную функции.

2. Найдите стационарные и критические точки второго рода, т. е. точки в которых вторая производная равна нулю или не существует.

3. Отметьте стационарные и критические точки второго рода на числовой прямой и определите знаки второй производной на получившихся промежутках.

4. Сделайте выводы о промежутках выпуклости, вогнутости и точках перегиба графика функции.

Схема исследования функции

1. Найдите область определения функции.

2. Определите четность, нечетность функции.

3. Найдите производную функции.

4. Определите стационарные и критические точки производной.

5. Определите промежутки монотонности и экстремумы функции.

6. Найдите значения функции в стационарных и критических точках.

7. Найдите вторую производную и исследуйте функцию на выпуклость и вогнутость.

8. Для построения графика найдите необходимые дополнительные точки.

Пример 4.

Исследуйте функцию и постройте график f(x)=3х²-х³

1. .

2. f(-x)=3(-х)²-(-х)³=3х²+х³ – функция общего вида, т.к. f(-x)≠ f(x) f(-x)≠ f(-x)

3. =(3х²-х³)=6х-3х²=3х(2-х)

4. =0, 3х(2-х)=0

х=0; х=2 – стационарные точки, критических точек нет

5. -

   -

   +

min

6. х=0 точка минимума, х=2 точка максимума

f(0)=0; f (2)= =4

7. 

=0, 6-6х=0

6(1-х)=0

х=1

-

+

‹ 0

› 0

х=1 – точка перегиба

f(1)= =2