2. Оптика Ортадағы жарық жылдамдығы

υ = c/n,

мұндағы, c – вакуумдағы жарық жылдамдығы; n – ортаның абсолют сыну көрсеткіші.

Жарық толқынының оптикалық жол ұзындығы

L = nl,

мұндағы, l – сыну көрсеткіші n ортадағы жарық толқынының геометриялық жол ұзындығы.

Екі жарық толқынының оптикалық жол айырымы

∆ = L₁ – L₂.

∆φ фазалар айырымы мен оптикалық жол айырымының арасындағы байланыс мынадай,

∆φ = 2π∆/λ

мұндағы, λ – жарық толқынының ұзындығы.

Интерференциялану кезінде жарықтың максималь күшею шарты мынадай,

∆ = kλ (k = 0, 1, 2, 3, …).

Интерференциялану кезінде жарықтың максималь әлсіреу шарты мына өрнекпен анықталады,

∆ = (2k + 1) (λ/2).

Монохромат жарықтың жұқа қабыршақтан шағылған кездегі жарық толқынының оптикалық жол айырымы,

немесе

∆ = 2dn cosi₂  λ/2,

мұндағы, d – пленканың (қабыршақтың) қалыңдығы; i₁ – түсу бұрышы, i₂ – сыну бұрышы, n – пленканың (қабыршақтың) сыну көрсеткіші.

Шағылған жарықтағы Ньютонның жарық сақиналарының радиусы (өткен жарық үшін қараңғы сақина),

(k = 1, 2, 3, …),

мұндағы k – сақина нөмері; R – линзаның қисықтық радиусы,

Шағылған жарықтағы Ньютонның қараңғы сақиналарының радиусы (өткен жарық үшін жарық сақина)

.

Сфералық толқын үшін Френельдің k –ші зонасының радиусы мынаған тең,

,

мұндағы, a – нүктелік жарық көзінен дөңгелек саңылауы бар диаграммаға дейінгі арақашықтық; b– дифракциялық көрініс бақыланатын экраннан диафрагмаға дейінгі қашықтық; k – Френель зонасының номері; λ–толқын ұзындығы.

Жазық толқын үшін,

.

Ьір саңлаудан алынған дифракцияның максимумына (жарық жолақ) сәйкес келетін сәулелердің ауытқу бұрышы мына шарт бойынша анықталады,

, (k = 1, 2, 3, …)

мұндағы, а – саңылаудың ені; φ – дифракция бұрышы; k – максимум номері; λ – толқын ұзындығы.

Дифракциялық тордан алынған дифракцияның максимумына (ашық жолақ) сәйкес келетін сәулелердің ауытқу бұрышы мына шарт бойынша анықталады,

dsinφ = kλ; (k = 0, 1, 2, 3, …)

мұндағы, d – дифракциялық тордың периоды.

Дифракциялық тордың ажыратқыштық қабілеті

,

мұндағы, ∆λ – дифракциялық тордың көмегімен алынған спектрде жекелей көруге болатын, екі көрші спектрлік сызықтардың (λ және λ + ∆λ) толқын ұзындықтарының ең кіші айырымы, N – тордың штрихтарының саны; k–дифракциялық максимумның реттік номері.

Вульф –Брэгг формуласы,

2dsin = kλ,

мұндағы, d – кристалдың атомаралық жазықтықтарының арақашықтығы;  –сырғанау бұрышы (кристалға түсетін рентген сәулесының параллель шоқтарының бағыты мен кристалдағы атомдық жазықтықтардың арасындағы бұрыш).

Брюстер заңы,

мұндағы, _В – диэлектриктен шағылған жарық толқыны толық поляризацияланған кездегі түсу бұрышы; n₂₁ – бірінші ортамен салыстырғандағы екінші ортаның салыстырмалы сыну көрсеткіші.

Малюс заңы,

I = I₀cos²α

мұндағы, I₀ – анализаторға түсетін жазық поляризацияланған жарықтың интенсивтілігі; I – осы жарықтың анализатор арқылы өткеннен кейінгі жазық поляризацияланған жарықтың интенсивтілігі; α – анализаторға түсетін толқынның жарық векторының тербеліс бағыты мен анализатордан өткізу жазықтығының арасындағы бұрыш (егер түсетін жарықтың электрлік векторының тербелісі осы жазықтықпен сәйкес келсе, онда анализатор түскен жарықты әлсіретпей өткізеді).

Оптикалық активті зат арқылы өткен кездегі монохромат жарықтың поляризация жазықтығының бұрылу бұрышы φ мына өрнекпен анықталады,

а) φ=[α]d (қатты заттарда),

мұндағы, α– айналу бұрышы; d– оптикалық активті заттағы жарықтың жүретін жолының ұзындығы;

б) φ = [α] ρ d (ерітінділерді),

мұндағы, [α] – меншікті айналу; ρ– ерітіндегі оптикалық активті заттардың массалық концентрациясы.

Релятивистік масса

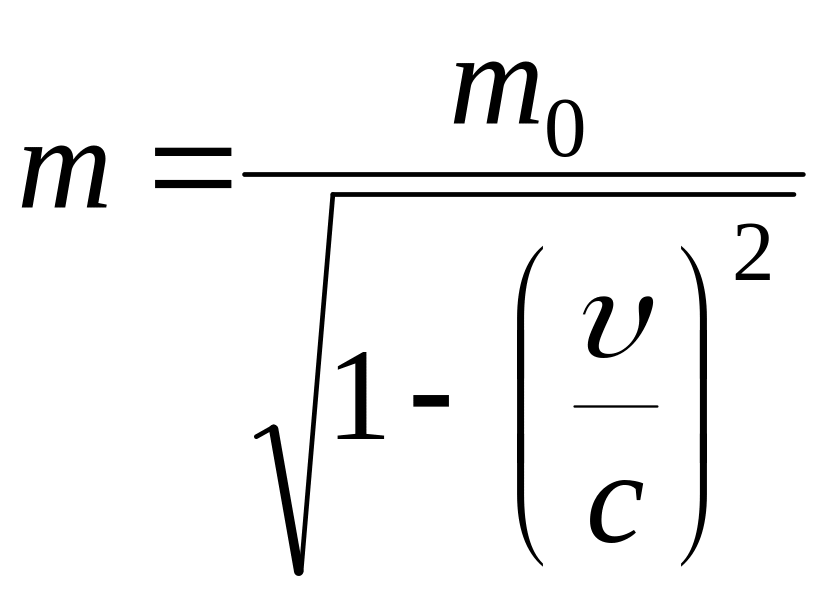немесе,

мұндағы, т₀ – бөлшектің тыныштық массасы; –оның жылдамдығы; с– жарықтың вакуумдағы жылдамдығы;  – жарық жылдамдығының бөлігі арқылы берілген бөлшектің жылдамдығы (=/с).

Релятивистік бөлшектің массасы мен энергиясы арасындағы өзара байланыс,

E=mc², немесе

Мұндағы, E₀=m₀ c²–бөлшектің тыныштық энергиясы.

Релятивистік бөлшектің кинетикалық энергиясы,

T=(m–m₀) c²_, немесе

Релятивистік бөлшектің импульсі

, немесе

Стефан-Больцман заңы

R_e = σT⁴,

мұндағы, R_e – қара дененің энергетикалық жарықталынуы; T– термодинамикалық температура; σ – Стефан-Больцман тұрақтысы (σ = 5,67∙10^-8 Вт/(м К⁴ )).

Сұр дененің энергетикалық жарықталынуы

R_e = a_TσT⁴

мұндағы, a_T – сұр дененің жылулық сәулелену коэффициенті (қаралану дәрежесі).

Виннің ығысу заңы

λ_m = b/T

мұндағы, λ_m – сәулеленудің максимум энергиясына сәйкес келетін толқын ұзындығы; b – Виннің тұрақтысы (b = 2,90∙10^-3 м∙K).

Фотонның энергиясы

ε = hν = hc/λ, немесе ε = ω,

мұндағы, h – Планк тұрақтысы; = h/(2π); ν – фотонның жиілігі; ω –циклдік жиілігі; λ – толқын ұзындығы.

Фотонның массасы,

;

Фотонның импульсі мына формуламен өрнектеледі:

.

Фотоэффекті үшін Эйнштейн формуласы

ε= hν = A + T_max, немесе ω = A + T_max,

мұндағы, ε = hν = ω – металл бетіне түскен фотонның энергиясы; A – электронның металдан шығу жұмысы; T_max – фотоэлектронның максимал кинетикалық энергиясы.