I. Комплексные числа. Множества в комплексной плоскости.

1. Действия над комплексными числами.

Множеством комплексных чисел называют множество выражений вида , где х, y – действительные числа, i – символ, называемый мнимой единицей, на котором введены операции сложения и умножения по следующим правилам:

1) ;

2) .

Из определения следует равенство . Совокупность всех комплексных чисел обозначается символом . Введенные операции сложения и умножения обладают всеми свойствами операций сложения и умножения на множестве всех действительных чисел. Два комплексных числа и считаются равными, если и . Если , то х называют действительной частью, а y – мнимой частью числа z и пишут , . Множество всех действительных чисел можно рассматривать как подмножество множества – это комплексные числа, мнимая часть которых равна 0.

Разностью чисел и называют такое число , что , при этом пишут ; несложно убедиться, что . Частным от деления на называют корень уравнения 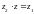; при этом пишут . Деление возможно лишь в том случае, когда делитель отличен от 0. Докажем это. Пусть и . Требуется найти такое, что

,

или

.

Приравнивая действительные и мнимые части выражений, приходим к системе линейных уравнений (относительно х и y):

Определитель этой системы , следовательно, эта система имеет единственное решение.

Множество комплексных чисел отождествляют с множеством векторов или множеством точек на плоскости с заданной декартовой прямоугольной системой координат; при таком отождествлении плоскость называют комплексной плоскостью. Число называют модулем числа z и обозначают . Угол между вектором и положительным направлением оси ОХ называют аргументом числа z и пишут . Модуль числа определяется однозначно, а аргумент может принимать бесконечно много значений, которые отличаются друг от друга на , . Обычно договариваются о главном значении аргумента; как правило, берут или .

Если и , то

, где

Если же , то

Аргумент числа не определен.

Из определения и следует, что

откуда получаем . Последнее равенство называется тригонометрической формой комплексного числа z (в отличие от алгебраической формы ).

Число называют сопряженным к числу , при этом пишут . Справедливы равенства:

; ; .

Операция сопряжения удобна при проведении деления чисел:

.

Введем обозначение:

.

Это равенство называется формулой Эйлера. Применив формулу Эйлера к тригонометрической форме числа, приходим к равенству ; это есть показательная форма числа z. В частности, , .

Справедливы равенства:

; ;

;

(равенства, связанные с , понимаются с точностью до ).

Тригонометрическая и показательная формы удобны при проведении операций умножения и деления комплексных чисел. Из выше перечисленных свойств следует формула Муавра в тригонометрической форме

и показательной форме

.

Число называется корнем n-й степени из числа , если . Любое отличное от 0 число имеет ровно n различных корней степени n; их находят по формулам

,

где k пробегает значения 0, 1, 2, … , ; – арифметический корень n-й степени из числа ρ.

Модуль разности чисел и равен расстоянию между точками и комплексной плоскости.

Пример 1. Выполнить действия: .

Решение. Представим числа , , в показательной форме.

Отсюда находим:

Такова показательная форма числа z. В тригонометрической форме результат имеет вид

Пример 2. Извлечь корень .

Решение. Представим число в тригонометрической форме:

Тогда:

, где

Отсюда находим четыре корня:

или

Пример 3. Изобразить на плоскости множество точек, удовлетворяющих условиям: а) ; б) ; в)

Решение. а) Перепишем уравнение в виде . Это уравнение окружности радиуса 1 с центром в точке .

б) Перепишем двойное неравенство в виде . Величина выражает расстояние от точки z до точки . Таким образом, двойное неравенство определяет кольцо с центром в точке , внутренний радиус которого равен 1, а внешний равен 3; при этом внутренняя окружность не принадлежит множеству, а внешняя принадлежит.

в) Первое условие задает кольцо с центром в точке , второе – угол, сторонами которого являются лучи и . В результате получаем сектор кольца.