
Вариант № 1
Пример № 1. Сложить матрицы A и B:
![]() ;
;
![]()
Пример № 2. Найти произведение матриц A и B (если это возможно):
![]() ;
;
![]()
Пример № 3. Найти определитель матрицы A:
![]()
Пример № 4. Найти определитель матрицы A:
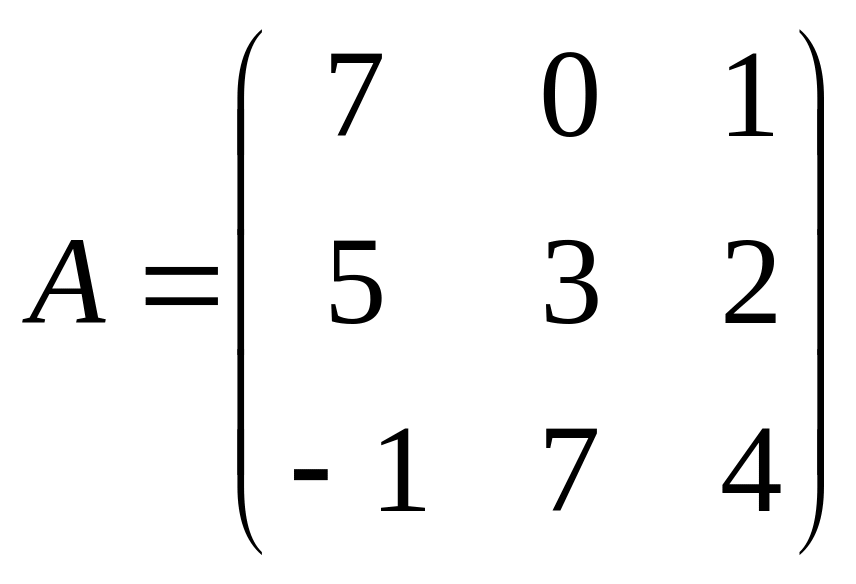
Пример № 5. Дана матрица A.
Найти миноры m11 и m32:
Пример № 6. Дана матрица A.
Найти алгебраические дополнения A11 и A32:
Пример № 7. Дана матрица A.
Найти обратную матрицу (если это возможно):
![]()
Пример № 8. При помощи элементарных преобразований над матрицами привести к каноническому виду матрицу A.
Определить ранг матрицы A.
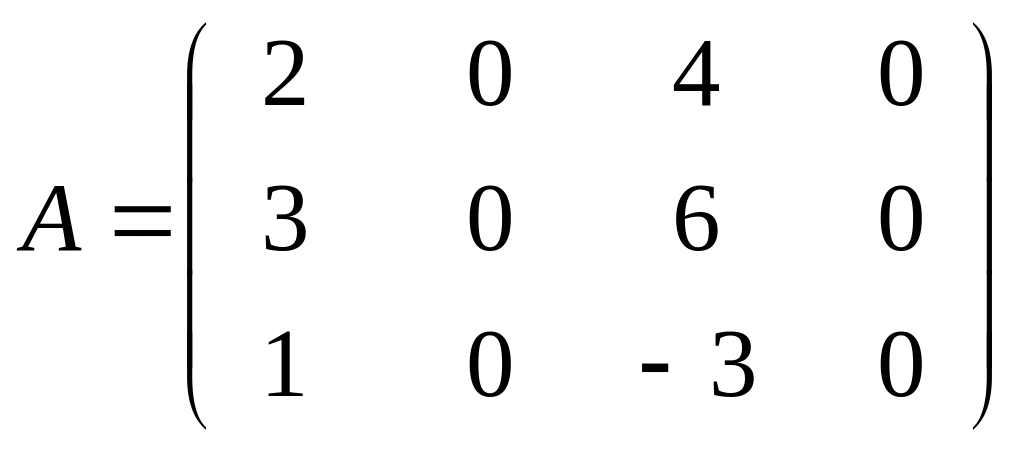
Пример № 9. Решить систему методом Крамера:
![]()
Пример № 10. Решить систему методом Гаусса:
![]()
Вариант № 2
Пример № 1. Сложить матрицы A и B:
![]() ;
;
![]()
Пример № 2. Найти произведение матриц A и B (если это возможно):
![]() ;
;
![]()
Пример № 3. Найти определитель матрицы A:
![]()
Пример № 4. Найти определитель матрицы A:
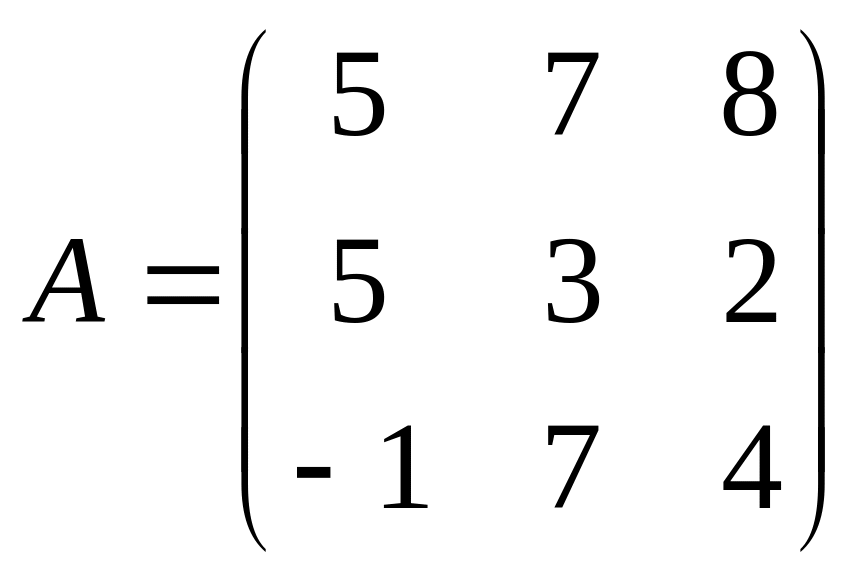
Пример № 5. Дана матрица A.
Найти миноры m11 и m32:
Пример № 6. Дана матрица A.
Найти алгебраические дополнения A11 и A32:
Пример № 7. Дана матрица A.
Найти обратную матрицу (если это возможно):
![]()
Пример № 8. При помощи элементарных преобразований над матрицами привести к каноническому виду матрицу A.
Определить ранг матрицы A.
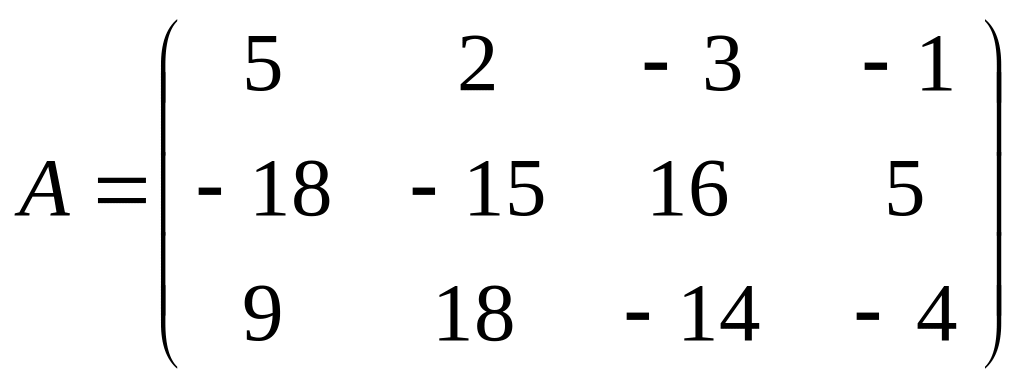
Пример № 9. Решить систему методом Крамера:
![]()
Пример № 10. Решить систему методом Гаусса:
![]()
Вариант № 3
Пример № 1. Сложить матрицы A и B:
![]() ;
;
![]()
Пример № 2. Найти произведение матриц A и B (если это возможно):
![]() ;
;
![]()
Пример № 3. Найти определитель матрицы A:
![]()
Пример № 4. Найти определитель матрицы A:
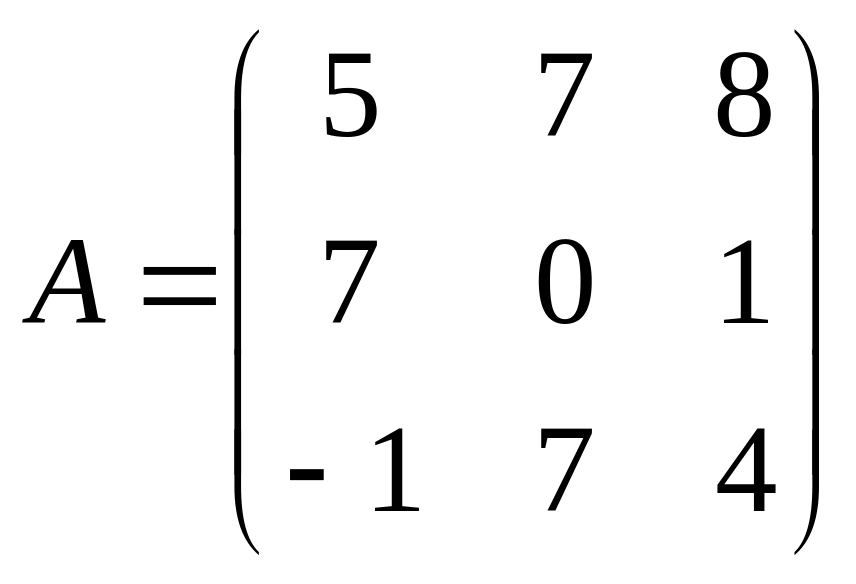
Пример № 5. Дана матрица A.
Найти миноры m11 и m32:
Пример № 6. Дана матрица A.
Найти алгебраические дополнения A11 и A32:
Пример № 7. Дана матрица A.
Найти обратную матрицу (если это возможно):
![]()
Пример № 8. При помощи элементарных преобразований над матрицами привести к каноническому виду матрицу A.
Определить ранг матрицы A.
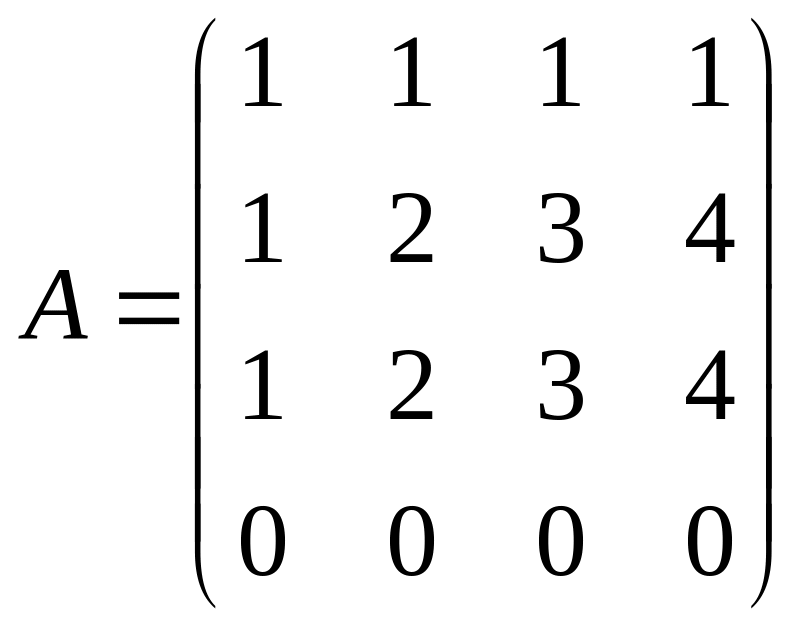
Пример № 9. Решить систему методом Крамера:
![]()
Пример № 10. Решить систему методом Гаусса:
![]()
Вариант № 4
Пример № 1. Сложить матрицы A и B:
![]() ;
;
![]()
Пример № 2. Найти произведение матриц A и B (если это возможно):
![]() ;
;
![]()
Пример № 3. Найти определитель матрицы A:
![]()
Пример № 4. Найти определитель матрицы A:
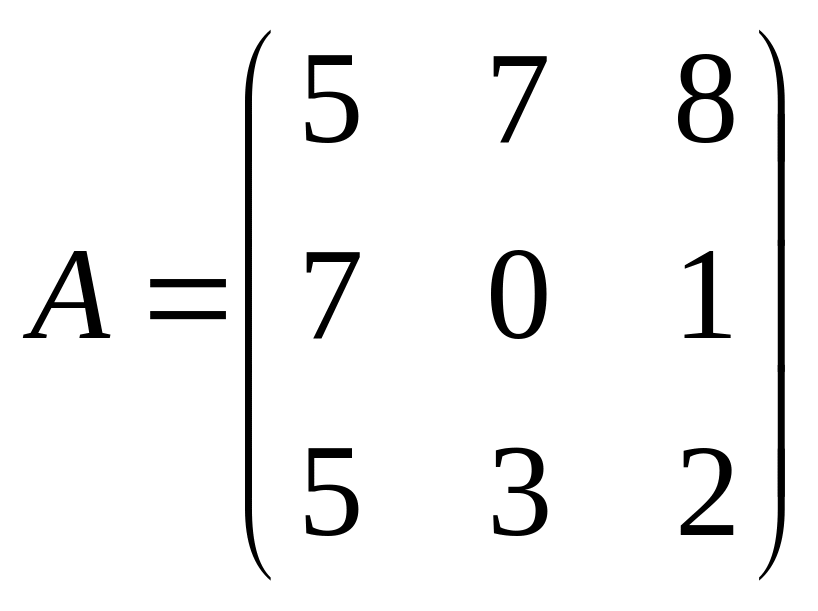
Пример № 5. Дана матрица A.
Найти миноры m11 и m32:
Пример № 6. Дана матрица A.
Найти алгебраические дополнения A11 и A32:
Пример № 7. Дана матрица A.
Найти обратную матрицу (если это возможно):
![]()
Пример № 8. При помощи элементарных преобразований над матрицами привести к каноническому виду матрицу A.
Определить ранг матрицы A.
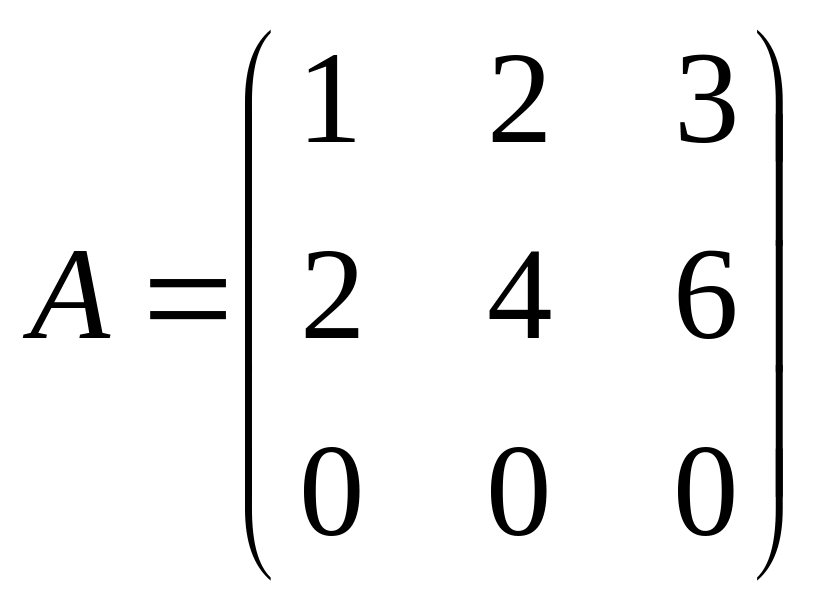
Пример № 9. Решить систему методом Крамера:
![]()
Пример № 10. Решить систему методом Гаусса:
![]()
