Метод математической индукции.

Метод математической индукции является важным способом доказательства предложений (утверждений), зависящих от натурального аргумента.

Метод математической индукции состоит в следующем:

Предложение (утверждение) P(n), зависящее от натурального числа n, справедливо для любого натурального n если:

1. P(1) является истинным предложением (утверждением);

2. P(n) остается истинным предложением (утверждением), если n увеличить на единицу, то есть P(n + 1) - истинное предложение (утверждение).

Таким образом, метод математической индукции предполагает два этапа:

1. Этап проверки: проверяется, истинно ли предложение (утверждение) P(1).

2. Этап доказательства: предполагается, что предложение P(n) истинно, и доказывается истинность предложения P(n + 1) (n увеличено на единицу).

Замечание. В некоторых случаях метод математической индукции используется в следующей форме: пусть m - натуральное число, m > 1 и P(n) - предложение, зависящее от n, n ≥ m. Если

1. P(m) справедливо;

2. P(n) будучи истинным предложением, влечет истинность предложения P(n + 1) для любого натурального n, n ≥ m, тогда P(n) - истинное предложение для любого натурального n, n ≥ m.

Ниже будут разобраны различные примеры использования математической индукции.

Задача о ханойской башне.

Задача состоит в том, чтобы переместить всю башню из 8 дисков на один из других колышков, перенося каждый раз только один диск и не помещая больший на меньший.

Наилучший способ разрешить вопрос, подобный нашему,— несколько обобщить его. Посмотрим, что будет в случае n дисков. Одно из преимуществ такого рода обобщения состоит в том, что можно будет даже еще уменьшить размер задачи. Полезно вначале рассмотреть крайние случаи. Совершенно ясно, как перемещать башню, состоящую только из одного или двух дисков, а после нескольких попыток становится понятно, как перемещать башню из трех дисков. Следующий шаг в решении задачи —выбор подходящего обозначения: обозначай и властвуй. Будем говорить, что Т_n есть минимальное число перекладываний, необходимых для перемещения n дисков с одного колышка на другой по правилам . Тогда T₁, очевидно, равно 1, а Т₂ равно 3. Можно получить дополнительную информацию, причем совершенно бесплатно, если рассмотреть самый крайний случай: ясно, что Т₀ = 0, поскольку для перемещения башни из n=0 дисков вообще не требуется ни одного перекладывания! Как переместить высокую башню? Эксперименты с тремя дисками показывают, что решающая идея состоит в переносе двух верхних дисков на средний колышек; затем переносится третий диск и на него помещаются два других. Это дает ключ к общему правилу перемещения n дисков: сначала мы перемещаем n— 1 меньших дисков на любой из колышков (что требует T_n-1 перекладываний), затем перекладываем самый большой диск (одно перекладывание) и, наконец, помещаем n— 1 меньших дисков обратно на самый большой диск (еще T_n-1 перекладываний). Таким образом, n дисков (при n > 0) можно переместить самое большее за 2T_n-1 + 1 перекладываний: T_n <= 2T_n-1 + 1. Более короткого пути нет. На некотором этапе мы обязаны переместить самый большой диск. Когда мы это делаем, n — 1 меньших дисков должны находиться на одном колышке, а для того, чтобы собрать их вместе, потребуется по меньшей мере T_n-1 перекладываний. Самый большой диск можно перекладывать и более одного раза, если мы не очень расторопны. Но после перемещения самого большого диска в последний раз мы обязаны поместить n — 1 меньших дисков (которые опять должны находиться на одном колышке) обратно на наибольший диск, что также требует T_n-1 перекладываний. Следовательно¸ T_n >=2T_n-1 + 1. Это значит, что T_n =2T_n-1 + 1. 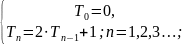(1.1) - совокупность подобных равенств называется рекуррентным соотношением. Найдём прямую формулу. T₀ = 0, T₁ = 1, T₂ = 3, T₃ = 7, T₄ = 15, T₅= 31, T₆ = 63. Очень похоже на 2ⁿ-1. Для произвольного номера n это можно доказать с помощью метода математической индукции. В нашем случае база индукции тривиальна, поскольку Т₀ = 2⁰ —1 = 0, а индуктивный переход выполняется для n > 0, когда n заменяется на n — 1: T_n = 2T_n-1 + 1 = 2(2^n-1-1)+ 1 = 2ⁿ-1. Следовательно, общая формула доказана для любого n =1,2,3….