Тема 4. Введение в математический анализ.

Понятие функции. Предел функции. Односторонние пределы. Предел функции при х→∞. Бесконечно малые и бесконечно большие функции, связь между ними. Основные теоремы о пределах. Первый и второй замечательный пределы. Непрерывность функции. Свойства функций, непрерывных на отрезке. Точки разрыва и их классификация.

Литература: [1, гл.2 §2-11], [4, гл.4 §2-9].

Вопросы для самоконтроля

1. Что называется пределом функции.

2. Бесконечно малые и бесконечно большие функции.

3. Раскрытие неопределенностей 0/0 и ∞/∞.

4. Первый и второй замечательный пределы, их следствия.

5. Дать определение непрерывности функции.

6. Точки разрыва и их классификация.

Тема 5. Дифференциальное исчисление

Производная функции, ее геометрический смысл. Основные правила и формулы дифференцирования. Производная сложной, обратной функции. Производные высших порядков. Некоторые теоремы о дифференцируемых функциях. Приложения производной. Правило Лопиталя. Условия монотонности функций. Необходимое и достаточное условия экстремума. Выпуклость и вогнутость, точки перегиба графика функции. Асимптоты. Общая схема исследования функции.

Литература:[1, гл.3 §2-16, гл.5 §2-11], [4, гл.5 §1-7, гл.6 §2,4], [2, гл.7 §1,2].

Вопросы для самоконтроля

1. Дать определение производной функции, ее геометрический и физический смысл.

2. Сформулировать основные правила дифференцирования.

3. Основные приложения производной.

4. Как определить промежутки монотонности и экстремумы функции.

5. Сформулировать необходимое и достаточное условия экстремума.

6. Определение выпуклости и вогнутости, точек перегиба графика функции.

7. Нахождение асимптот графика функции.

3 Контрольные работы

Программой дисциплины «Математика» для студентов I курса в первом семестре предусмотрено выполнение одной контрольной работы.

При выполнении контрольной работы необходимо изучить элементы линейной и векторной алгебры, аналитической геометрии на плоскости и в пространстве, а также ознакомиться с теорией кривых второго порядка и комплексными числами. Необходимо научиться вычислять основные типы пределов - неопределенности , первый и второй замечательный пределы. Изучить понятие непрерывности функции, основы дифференциального исчисления функции одной переменной, а также их приложения к исследованию функции.

Ниже приведены примеры выполнения расчетов.

К заданиям 1-10

Пример. Доказать, что векторы линейно независимы и найти разложение вектора по векторам .

Решение. , . Покажем, что векторы - некомпланарны. Для этого найдем их смешанное произведение:

= = 1 – 18 - 0 - 4 - 0- 3 = - 24.

Так как смешанное произведение отлично от нуля, то векторы линейно независимы. Найдем разложение вектора по векторам , т.е. , где - неизвестные величины; для нахождения этих величин составим систему трех уравнений:

=

.

Решим эту систему методом Гаусса. Первое уравнение оставим без изменения, для получения второго сложим два первых, а третье сложим с первым, умножим на (-2):

<=> .

Первые два уравнения последней системы оставим без изменения, а третье сложим со вторым:

<=> <=> .

Таким образом, .

Ответ: .

К заданиям 11-20 По координатам вершины пирамиды А₁А₂А₃А₄ найти:

1. длину ребра А₁А₂;

2. угол между ребрами А₁А₂ и А₁А₄;

3. площадь грани А₁А₂А₃;

4. объем пирамиды;

5. уравнения плоскостей А₁А₂А₃ и А₁А₂А₄ ;

6. угол между плоскостями А₁А₂А₃ и А₁А₂А₄.

1) Если заданы точки A₁(x₁, y₁, z₁) , А₂(x₂, y₂, z₂), то координаты вектора:

тогда длина вектора вычисляется по формуле .

2) Из определения скалярного произведения следует, что угол между векторами вычисляется по формуле

.

3) - площадь треугольника, построенного на векторах и .

4) Учитывая геометрический смысл смешанного произведения векторов, получим формулу вычисления объема пирамиды : .

5) Если даны три точки А₁(x₁; y₁; z₁), А₂(x₂; y₂; z₂) и А₃(x₃; y₃; z₃), то уравнение плоскости, проходящей через три точки, находится по формуле

(1)

Например

Составить уравнение плоскости, проходящей через три точки А₁ , А₂ ,А₃, если А₁(-3, 2, 0), А₂(-2, 0, 2), А₃(0, 3, -1).

Решение: по формуле (1) получим ,

Итак, уравнение плоскости имеет вид −4х+7у+7z-26=0, где нормаль имеет координаты N(-4; 7; 7).

6) Угол, образованный двумя плоскостями, находится по формуле

где - нормали плоскостей.

К заданиям 21-30

Пример. Найти уравнение данной кривой в декартовой системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью: .

Связь между полярными и прямоугольными координатами точки устанавливаются формулами:

По условию , имеем ;

; ;

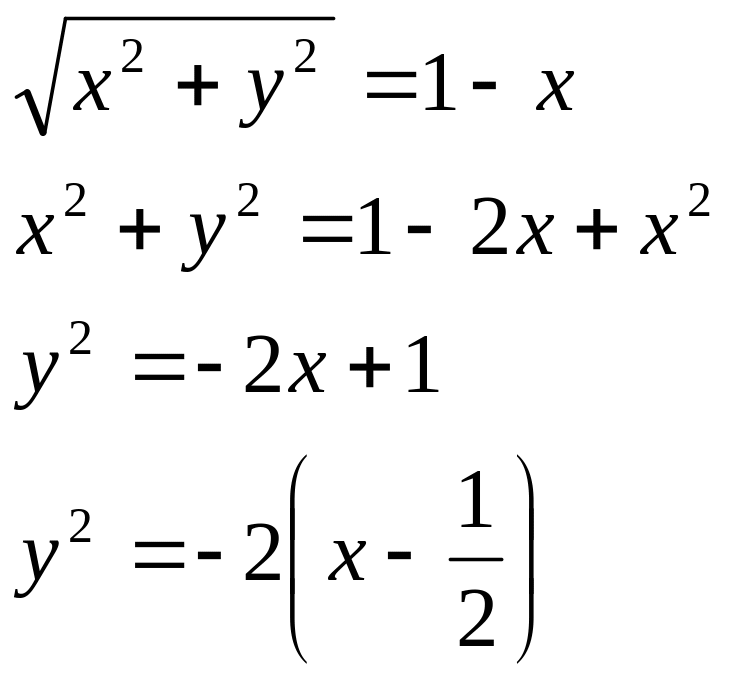
Это каноническое уравнение параболы с вершиной в точке .

К заданиям 31-40 Найти решение системы с помощью правила Крамера

Для систем трех уравнений с тремя неизвестными

правило Крамера имеет вид: ,

где

Определитель третьего порядка, обозначаемый символом

∆= ,

вычисляется по правилу треугольника:

.

Например

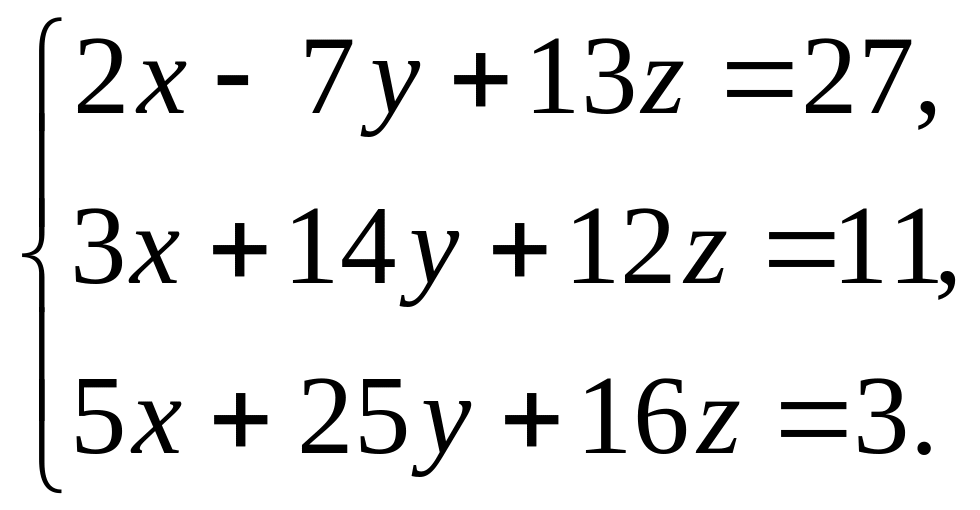
Решение.

.

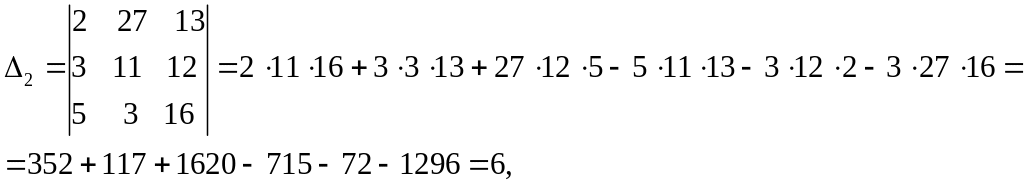
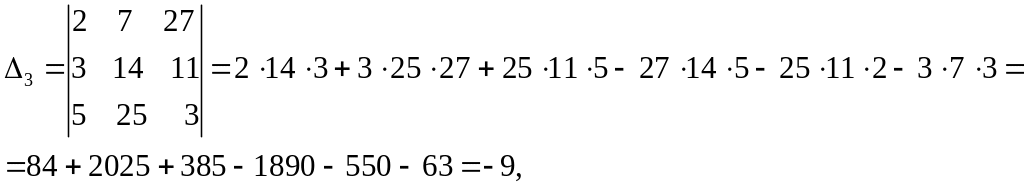
Ответ: (1, -2, 3).

Применение метода Гаусса приведено в примере к заданиям 1-10.

К заданиям 41 ‑ 50

Пример. Представить число в алгебраической форме.

Решение.

.

Пример. Представить число 1+i в тригонометрической форме.

Решение

Вычислим модуль

.

Найдем аргумент из системы уравнений

Поделим второе уравнение на первое, получим

Системе уравнений удовлетворяет значение Следовательно, тригонометрическая форма имеет вид

.

К заданиям 51-60

Вычислить пределы функций, не пользуясь правилом Лопиталя.

При вычислении предела дробно-рациональной функции при числитель и знаменатель дроби—величины бесконечно большие, т.е. получаем выражение которое представляет собой неопределённость. Для вычисления предела этой функции нужно числитель и знаменатель дроби разделить на наивысшую степень х.

Пример 1.

Решение. Для вычисления предела этой функции нужно числитель и знаменатель разделить на :

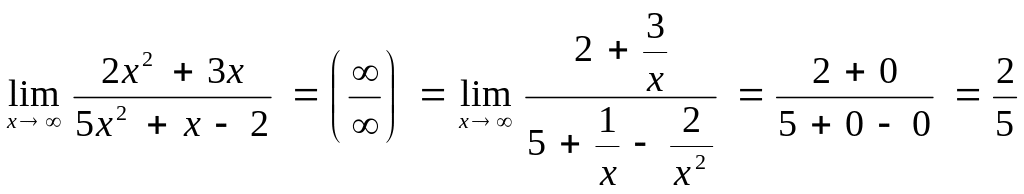
(при слагаемые — величины бесконечно малые и, следовательно, их пределы равны нулю).

В том случае, когда при вычислении предела дробно-рациональной функции при числитель и знаменатель имеют предел, равный нулю, т.е. имеем неопределенность , надо разделить их на и перейти к пределу. Если после деления окажется, что при числитель и знаменатель снова имеют пределы, равные нулю, то надо произвести повторное деление на .

Пример 2.

.

Здесь мы имеем неопределенность вида . Домножим числитель и знаменатель дроби на выражение, сопряженное числителю (избавимся от иррациональности в числителе):

.

При вычислении пределов тригонометрических функций часто используется первый замечательный предел и его следствия:

Пример 3.

Решение. Преобразовав разность косинусов в произведение, получим

Если в пределе получаем неопределенность , используем второй замечательный предел (2)

Пример 4.

Решение. Выполнив преобразования и применив второй замечательный предел, найдём

Пример 5.

Решение. Выполнив преобразования и применив формулу (2), найдём

К заданиям 61-70

Пример. Задана функция . Найти точки разрыва и определить их тип. Сделать схематический чертеж.

если <1,

если

если >2.

Решение. Функции , непрерывны на всей числовой прямой, поэтому данная функция может иметь разрывы только в точках, где меняется ее аналитическое выражение, т.е. в точках и .

Исследуем функцию на непрерывность в этих точках, для чего найдем соответствующие односторонние пределы и значения функции. В точке ,

. Таким образом,

. Значит функция непрерывна в точке .

В точке , .

Таким образом, , т.е. функция имеет разрыв Ι рода и непрерывна слева. Скачок функции в точке равен ∆ .

График функции изображен на рисунке

К заданиям 71-80

При выполнении данного задания необходимо знать правила вычисления производной (производная суммы, произведения и частного дух функций), а также изучить таблицу производных.

Пример. Найти производные данных функций.

а).

б).

.

в).

.

г).

Прологарифмируем обе части равенства . Тогда , т.е. . Теперь продифференцируем последнее равенство

, т.е. или .

Отсюда . Учитывая, что , имеем .

д). .

Дифференцируя обе части уравнения и учитывая, что - есть функция от (поэтому, например, ), получим или

Отсюда находим : или

т.е. .

К заданиям 81-90

Пример. Применяя формулу Тейлора с остаточным членом в форме Лагранжа к функции , вычислить значение с точностью до 0,0001. a=0,5.

Решение. Применив разложение , получаем

.

Определим число n так, чтобы погрешность приближенного равенства не превышала 0,0001. Погрешность этого равенства определяется суммой членов, следующих после в разложении :

.

< .

Просуммируем бесконечно убывающую геометрическую прогрессию в квадратных скобках:

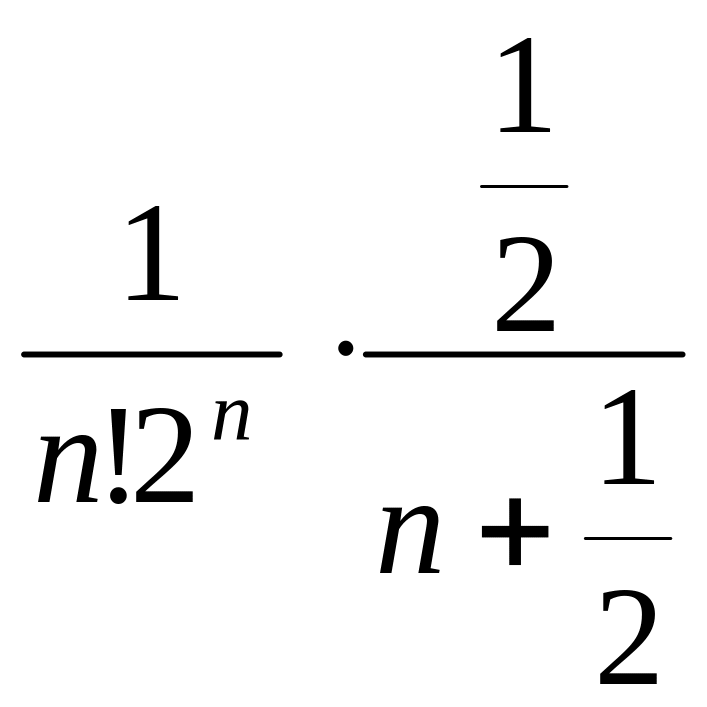< . Полагаем , тогда < , т.е. < . Путем подбора определяем, при каком значении будет выполняться <0,0001. Получаем, что при

< , <0,0001. Итак, принимаем .

.

К заданиям 91-100 и 101-110

Общая схема исследования функции и построения графика.

1. Найти область определения функции.

2. Определить тип функции (четность, нечетность).

3. Найти точки пересечения с осями координат и интервалы

знакопостоянства функции.

4. Найти асимптоты графика функции:

а) вертикальные; б) невертикальные (наклонные).

5. Найти точки возможного экстремума и интервалы возрастания и

убывания функции.

6. Найти точки перегиба и интервалы выпуклости, вогнутости функции.

7. Найти дополнительные точки.

8. Построить график функции, учитывая проведенные исследования.

Пример. Исследовать функцию и построить ее график.

Решение

1. , .

Область определения функции: .

Точки разрыва: .

2. . Так как , то функция нечетная. Следовательно, ее график симметричен относительно точки О.

3. .

			0
знак	+	-	0	+	-
Расположение графика	Выше оси Ох	Ниже оси Ох	Пересекает ось Ох	Выше оси Ох	Ниже оси Ох

4. а). Вертикальные асимптоты:

; .

Следовательно, - точка разрыва второго рода. По свойству симметрии функции . Поэтому уравнения вертикальных асимптот и .

Других вертикальных асимптот график не имеет.

б). Наклонные асимптоты :

;

.

Итак, - уравнение наклонной асимптоты графика функции.

5. .

, , - критические точки.

не существует при , поэтому не является критическими точками.

X		-3			0			3
	-	0	+	+	0	+	+	0	-
		4,5 min			Нет экст.			-4,5 max

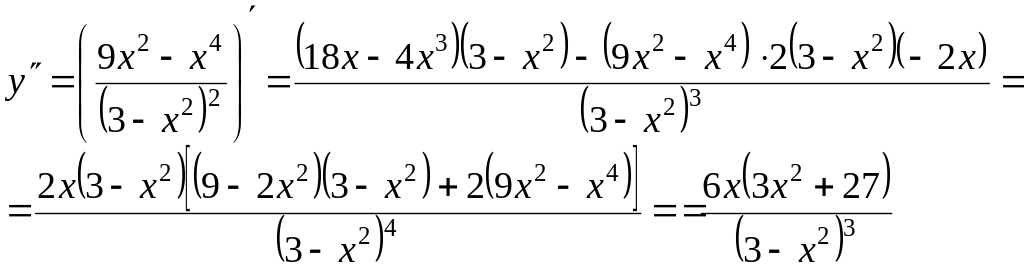
6. ; при критическая точка.

не существует при . Следовательно, имеется одна критическая точка .

			0
	+	-	0	+	-
			0

7. Дополнительные точки

	0,5	1	1,5	2	3,5	4
	0,05	0,5	4,5	-8	-4,6	-5

8.Строим график функции.