
- •Розділ 1. Елементи лінійної алгебри
- •Тема 1: Обчислення визначників 4-го й вищих порядків. Мінори та алгебраїчні доповнення.
- •Короткі теоретичні відомості
- •1) Віднімемо від елементів 1-го стовпця відповідні елементи 4-го
- •2) Віднімемо від елементів 4-го рядка відповідні елементи 2-го
- •Питання для контролю вивченого матеріалу
- •Література
- •Тема 2: Методи розв’язування систем лінійних рівнянь.
- •Короткі теоретичні відомості
- •Питання для контролю вивченого матеріалу
- •Література
- •Назієв е.Х., Владіміров в.М., Миронець о.А. Лінійна алгебра та аналітична геометрія. – к.: Лебідь, 1997. – 151 с.
- •Соколенко о.І. Вища математика. – к.: Видавничий центр „Академія”, 2002. – 431с.
- •Тема 3: Розв’язування довільних лінійних систем. Теорема Кронекера-Капеллі. Системи однорідних лінійних рівнянь.
- •Короткі теоретичні відомості
- •Питання для контролю вивченого матеріалу
- •Література
- •Розділ 2. Елементи векторної алгебри та аналітична геометрія
- •Тема 1: Системи координат на прямій, на площині, в просторі. Вектори в системі координат.
- •Короткі теоретичні відомості
- •Питання для контролю вивченого матеріалу
- •Література
- •Тема 2: Скалярний добуток векторів.
- •Короткі теоретичні відомості
- •Питання для контролю вивченого матеріалу
- •Література
- •Тема 3: Мішаний добуток трьох векторів. Об’єм тетраедра.
- •Короткі теоретичні відомості
- •Питання для контролю вивченого матеріалу
- •Література
Розділ 2. Елементи векторної алгебри та аналітична геометрія
Тема 1: Системи координат на прямій, на площині, в просторі. Вектори в системі координат.
Системи координат на прямій, на площині, в просторі.
Основні поняття про вектор.
Вектори в системі координат. Розклад вектора за базисом.
Короткі теоретичні відомості
Система координат – це сукупність умов, за допомогою яких визначається положення точки на прямій, на площині, в просторі.
Координатою
точки
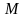 на
прямій зветься відстань
на
прямій зветься відстань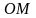 ,
що вимірюється масштабною одиницею,
взятою із знаком “+”, якщо напрям від
точки
,
що вимірюється масштабною одиницею,
взятою із знаком “+”, якщо напрям від
точки
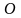 до
точки
збігається
з додатним напрямом на прямій, і з знаком
“-“, якщо ці напрями протилежні. Відстань
між точками
до
точки
збігається
з додатним напрямом на прямій, і з знаком
“-“, якщо ці напрями протилежні. Відстань
між точками
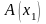 та
та
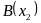 на прямій визначається таким чином:
на прямій визначається таким чином:
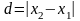 . (1)
. (1)
Система координат на площині зветься
прямокутною декартовою, якщо осі
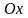 і
і
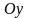 взаємно перпендикулярні і мають однакові
масштабні одиниці (мал.1).
взаємно перпендикулярні і мають однакові
масштабні одиниці (мал.1).
Якщо
спроектуємо точку
на осі
та
,
то
має
на осі
координату
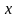 (абсцису),
а на осі
координату
(абсцису),
а на осі
координату
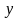 (ординату).
(ординату).
Відстань
від точки
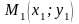 до точки
до точки
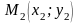 знайдемо за формулою
знайдемо за формулою
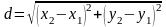 . (2)
. (2)
Цілком
аналогічно у просторі, проектуючи точку
на
взаємно перпендикулярні осі
,
,
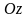 ,
що мають однакові масштабні одиниці,
маємо відповідно абсцису, ординату та
аплікату точки
(мал.2).
,
що мають однакові масштабні одиниці,
маємо відповідно абсцису, ординату та
аплікату точки
(мал.2).
Відстань
між точками
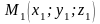 та
та
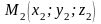 визначається за формулою
визначається за формулою
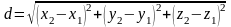 . (3)
. (3)
Будемо називати вектором напрямлений прямолінійний відрізок. Довжину відрізка, який зображує вектор, називають модулем або довжиною вектора. Якщо модуль вектора дорівнює нулю, то вектор буде нульовим і напрям його невизначений.
Вектори, які лежать на одній прямій або на паралельних прямих, називають колінеарними. Якщо ж вони до цього мають однаковий напрям, то їх називають співнапрямленими. Колінеарні вектори, що мають протилежні напрями, називають протилежно напрямленими. Вектори, що лежать на одній або паралельних площинах, називають компланарними. Якщо вектори співнапрямлені і мають однакові модулі, то такі вектори називають рівними. Якщо вектори мають однакові модулі, але протилежно напрямлені, то їх називають протилежними.
Сумою n векторів, розміщених послідовно, називають вектор, який сполучає початок першого вектор-доданка з кінцем останнього вектор-доданка. Якщо два вектори мають спільний початок, то для знаходження суми таких двох векторів необхідно побудувати на них паралелограм. Вектор, який збігається з діагоналлю побудованого паралелограма, що має спільний початок із заданими векторами, буде сумою цих векторів. Це правило додавання двох не колінеарних векторів називають правилом паралелограма.
Різницею
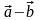 двох векторів
двох векторів
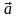 і
і
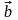 називають такий третій вектор
називають такий третій вектор
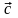 ,
який треба додати до вектора
,
щоб дістати вектор
,
отже,
,
який треба додати до вектора
,
щоб дістати вектор
,
отже,
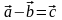 ,
якщо
,
якщо
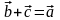 .
.
Добутком вектора
на дійсне число (скаляр)
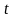 називають
такий вектор
,
модуль якого дорівнює
називають
такий вектор
,
модуль якого дорівнює
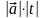 і який колінеарний з вектором
і однаково напрямлений з ним при
і який колінеарний з вектором
і однаково напрямлений з ним при
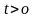 та протилежно напрямлений при
та протилежно напрямлений при
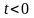 і є нуль-вектором при
і є нуль-вектором при
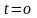 .
.
Розділити вектор
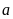 на дійсне число
на дійсне число
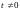 означає помножити вектор
на число
означає помножити вектор
на число
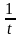 ,
тобто
,
тобто
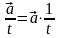 .
.
Одиничним вектором вектора (або ортом вектора) називають вектор, довжина якого дорівнює одиниці і який співнапрямлений з даним вектором.
Якщо маємо вектор у системі координат, то це означає, що задано його координати, тобто алгебраїчні проекції вектора на відповідні осі координат.
Нехай
маємо прямокутну декартову систему
координат у просторі. Координати вектора
позначимо через
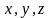 .
Тоді будемо записувати
.
Тоді будемо записувати
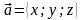 .
.
Очевидно,
що
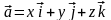 , (4)
, (4)
де
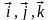 - одиничні вектори, взяті відповідно за
осями координат. Трійка векторів
- одиничні вектори, взяті відповідно за
осями координат. Трійка векторів
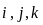 утворює координатний базис, якщо вектор
утворює координатний базис, якщо вектор
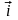 належить осі
,
вектор
належить осі
,
вектор
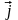 - осі
,
вектор
- осі
,
вектор
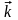 - осі
.
Кожен з векторів
має напрям, що збігається з додатним
напрямом відповідної осі, якій він
належить. Подання вектора
у вигляді (4) є розкладом вектора
за координатним базисом
.
- осі
.
Кожен з векторів
має напрям, що збігається з додатним
напрямом відповідної осі, якій він
належить. Подання вектора
у вигляді (4) є розкладом вектора
за координатним базисом
.
Якщо вектор
має координати
,
то його модуль визначається за формулою
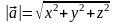 . (5)
. (5)
Якщо маємо дві точки
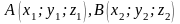 ,
то координати вектора
,
то координати вектора
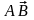 визначаються так:
визначаються так:
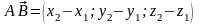 . (6)
. (6)
Якщо вектори колінеарні, то їх координати пропорційні.
Приклад.
Обчислити
при яких значеннях
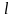 і
вектори
і
вектори
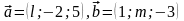 колінеарні.
колінеарні.
▲ Записавши
умову колінеарності даних векторів,
маємо
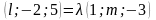 .
Так як у колінеарних векторів відповідні
координати пропорційні, маємо:
.
Так як у колінеарних векторів відповідні
координати пропорційні, маємо:
 .
Отже,
.
Отже,
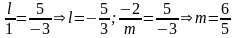 .
Отримали
.
Отримали
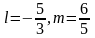 .▼
.▼
