Розділ 1. Елементи лінійної алгебри

Тема 1: Обчислення визначників 4-го й вищих порядків. Мінори та алгебраїчні доповнення.

1. Визначники довільного порядку.

2. Мінори та алгебраїчні доповнення.

Короткі теоретичні відомості

Визначником 4-го порядку називається визначник, який містить 4 рядки та 4 стовпці, тобто це визначник вигляду:

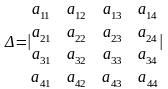(1)

Визначник 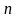-го порядку має слідуючи вигляд

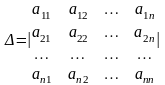(2)

Для визначників -го порядку справджуються властивості визначників другого й третього порядку.

Приклад. Обчислити визначник

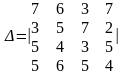
1) Віднімемо від елементів 1-го стовпця відповідні елементи 4-го

2) Віднімемо від елементів 4-го рядка відповідні елементи 2-го

3) Розкриваємо визначник за елементами 1-го стовпця

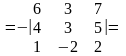
4) Віднімемо від елементів 1-го та 2-го рядків відповідні елементи 3-го рядка, помножені відповідно на 6 і 4

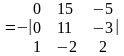
5) Розкриваємо визначник за елементами 1-го стовпця та обчислюємо його •

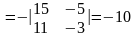Мінором 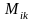, що відповідає елементу 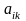матриці

(3)

називається визначник, який відповідає матриці, утвореній з матриці (3) викресленням i-го рядка та k-го стовпця.

Алгебраїчним доповненням 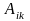елемента матриці (2.3) називається відповідний мінор. Взятий зі знаком плюс, якщо сума його індексів парна, і зі знаком мінус, якщо сума його непарна:

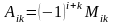(4)

Питання для контролю вивченого матеріалу

1. Що називається визначником квадратної матриці -го порядку?

2. Що називається мінором елемента матриці?

3. Що називається алгебраїчним доповненням?

4. Обчислити визначник

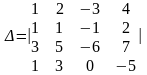
Література

1. Назієв Е.Х., Владіміров В.М., Миронець О.А. Лінійна алгебра та аналітична геометрія. – К.: Лебідь, 1997. – 151 с.

2. Соколенко О.І. Вища математика. – К.: Видавничий центр „Академія”, 2002. – 431с.

Тема 2: Методи розв’язування систем лінійних рівнянь.

1. Розв’язування систем лінійних рівнянь матричним методом.

2. Розв’язування систем лінійних рівнянь методом Гауса.

Короткі теоретичні відомості

Нехай дано систему лінійних рівнянь з невідомими

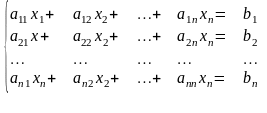(1)

Розглянемо матрицю системи

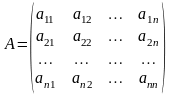
та матриці-стовпці невідомих і вільних членів , .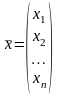

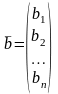Тоді систему (1) можна записати так 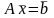(2).

Рівність (2) називається матричним рівнянням, яке відповідає системі рівнянь (1).

З рівності (2) слідує 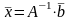(3).

Отже, щоб знайти розв’язок системи лінійних рівнянь з невідомими, визначник якої не дорівнює нулю, треба знайти обернену матрицю для матриці 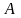системи і помножити на цю матрицю зліва стовпчик вільних членів. В результаті дістанемо стовпець-розв’язок системи рівнянь.

Приклад. Розв’язати матричним методом систему рівнянь

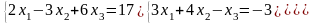
° Матриця цієї системи

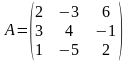
маємо обернену матрицю .

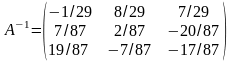Скориставшись рівністю (3), знаходимо

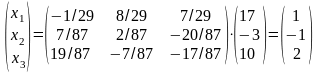, тобто 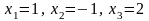шуканий розв’язок •

1. Найчастіше для розв’язування системи лінійних рівнянь застосовують метод виключення невідомих, що ґрунтується на так званих елементарних перетвореннях системи.

Елементарними перетвореннями системи лінійних рівнянь називається:

• переставляння рівнянь;

• множення обох частин рівняння на одне й те саме число, що не дорівнює нулю;

• додавання до обох частин якого-небудь рівняння відповідних частин другого рівняння, помноженого на довільне число.

Метод Гауса виключення невідомих полягає в тому, що за допомогою елементарних перетворень дана система перетворюється на тотожну їй систему, але простішого вигляду, з якої розв’язки системи видно безпосередньо. Наприклад, система (1) при

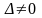
За допомогою елементарних перетворень завжди може бути перетворена на тотожну їй систему так званої трикутної форми:

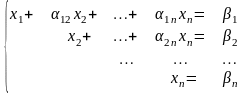
З цієї системи послідовно, починаючи з останнього рівняння, знаходять .

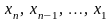Приклад. За допомогою елементарних перетворень звести систему 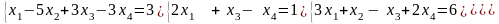до трикутного вигляду й знайти її розв’язки.

° Оскільки невідомі в елементарних перетвореннях не беруть участі їх на деякий час залишають осторонь і виконують перетворення над коефіцієнтами і вільними членами системи, розміщуючи у вигляді розширеної матриці системи точно так, як вони розміщені у системі.

Розширена матриця даної системи має вигляд 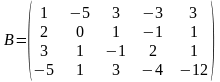, де вертикальною рискою відокремлені вільні члени системи. Тепер задача зводиться до того, щоб матрицю системи, розміщену ліворуч від вертикальної риски, привести до трикутного вигляду.

Виконаємо над матрицею 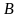такі перетворення:

1. додамо до елементів 2-го, 3-го, 4-го рядків відповідні елементи 1-го рядка, помноженого послідовно на -2, -3 і 5

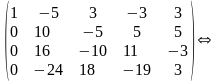
2. скорочуємо елементи 2-го рядка на 5 і помноживши їх послідовно на -8 і 12, додаємо до відповідних елементів 3-го та 4-го рядків

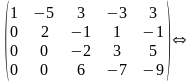
3. елементи третього рядка, помножені на 3, додаємо до елементів 4-го; в результаті дістанемо матрицю системи лінійних рівнянь, рівносильну початковій системі

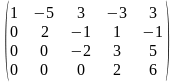
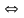
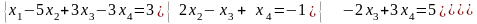
З даної системи послідовно знаходимо •
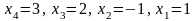