
- •Лабораторна робота №1 Обчислення похибок фізичних вимірювань. Визначення густини тіл правильної геометричної форми
- •Теоретичні відомості
- •Правила оцінювання похибки прямих вимірювань
- •Правила оцінювання похибки непрямих вимірювань
- •Метод визначення густини
- •Порядок виконання та обробка результатів вимірювань
- •Контрольні запитання
Метод визначення густини
У
цій роботі визначається густина
циліндричного зразка за результатами
вимірювань його маси та розмірів:
 - діаметра,
- діаметра,
 - висоти.
- висоти.
Густиною
однорідного тіла називається відношення
маси тіла до його об’єму:
 ,
або,
іншими словами, густина визначає масу
одиниці об’єму.
,
або,
іншими словами, густина визначає масу
одиниці об’єму.
Маса є мірою інертних і гравітаційних властивостей тіла і є величиною скалярною та адитивною (маса складеного тіла дорівнює сумі мас усіх його частин).
Об’єм циліндричного зразка:

Тоді густина твердого циліндричного зразка визначається за формулою:

Дана
формула може бути записана у вигляді
 .
Щоб дістати співвідношення для визначення
відносної похибки спочатку даний вираз
логарифмується:
.
Щоб дістати співвідношення для визначення
відносної похибки спочатку даний вираз
логарифмується:

Потім обчислюються частинні похідні:

Підставивши ці значення частинних похідних у рівняння (1.3), отримаємо формулу для обчислення відносної похибки:
 .
.
Після
обчислення відносної похибки
 абсолютна похибка обчислюється за
формулою:
абсолютна похибка обчислюється за
формулою:
 .
.
Остаточний результат непрямих вимірювань записується у вигляді:
 .
.
Похибка
сталої величини
 не входить до розрахункової формули,
оскільки її можна зробити як завгодно
малою. З якою же кількістю знаків доцільно
брати число
?
При округленні трансцедентного числа
не входить до розрахункової формули,
оскільки її можна зробити як завгодно
малою. З якою же кількістю знаків доцільно
брати число
?
При округленні трансцедентного числа
 ,
тобто замінюючи його значення наближеним,
ми вносимо відносні похибку:
,
тобто замінюючи його значення наближеним,
ми вносимо відносні похибку:


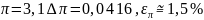

Нагадаємо,
що відносна похибка, яка знаходиться у
результаті обчислень, має бути приблизно
на порядок (тобто у 10 разів) менша за
похибку результату непрямих вимірювань.
Тому, оскільки похибка непрямих вимірювань
у навчальній лабораторії становить
декілька відсотків, то число
будемо брати з трьома значущими цифрами,
тобто
 .
.
Порядок виконання та обробка результатів вимірювань
1.
Вибрати з таблиці 1.1. виміряні значення
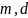 і
,
що відповідають номеру бригади, та
записати їх в таблицю 1.2.
і
,
що відповідають номеру бригади, та
записати їх в таблицю 1.2.
Таблиця 1.1
Номер бригади |
№ виміру |
Діаметр , мм
|
Висота
|
Маса
|
1 |
1 2 3 4 5 |
12,50 12,51 12,53 12,49 12,52 |
18,95 18,90 18,90 18,85 18,95 |
18,17 18,15 18,14 18,14 18,18 |
2 |
1 2 3 4 5 |
18,32 18,31 18,30 18,31 18,32 |
32,10 32,05 32,15 32,10 32,15 |
6,705 6,702 6,701 6,706 6,703 |
3 |
1 2 3 4 5 |
9,31 9,30 9,32 9,29 9,27 |
13,15 13,05 13,10 13,05 13,10 |
6,93 6,92 6,93 6,97 6,96 |
4 |
1 2 3 4 5 |
16,31 16,33 16,35 16,32 16,33 |
18,35 18,40 18,45 18,40 18,40 |
29,35 29,28 29,30 29,33 29,29 |
5 |
1 2 3 4 5 |
17,77 17,75 17,72 17,74 17,71 |
21,95 21,90 21,85 21,90 21,85 |
45,63 45,69 45,67 45,65 45,64 |
2. Провести обробку результатів прямих вимірювань, для цього розрахувати:
-
середні значення
 і
і
- відхилення від середніх значень
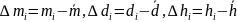 ;
;
- середні квадратичні відхилення

 .
.
Розрахунки виконати з чотирма значущими цифрами. Результати розрахунків записати до таблиці 1.2.
Таблиця 1.2
Номер виміру |
Маса зразка
|
Діаметр зразка , мм |
Висота зразка , мм |
Відхилення від середнього
|
||||
|
|
|
||||||
1 |
|
|
|
|
|
|
||
2 |
|
|
|
|
|
|
||
3 |
|
|
|
|
|
|
||
4 |
|
|
|
|
|
|
||
5 |
|
|
|
|
|
|
||
Середні значення |
Середньоквадратичні відхилення |
|||||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
3.
Визначити випадкові похибки
 .
Для цього середні квадратичні відхилення
.
Для цього середні квадратичні відхилення
 ,
помножити на коефіцієнт Стьюдента
,
помножити на коефіцієнт Стьюдента
 для даної надійної ймовірності
та кількості вимірювань
.
В даній роботі для
і
для даної надійної ймовірності
та кількості вимірювань
.
В даній роботі для
і

 .
.
4. Значення випадкових похибок округлюються до однієї значущої цифри, якщо перша цифра більша за 3. Якщо ж вона дорівнює 3 або менша, округлюється до двох значущих цифр. Наприклад, якщо обчислення дають значення 0,419 і 0,123, то після округлення отримуємо 0,4 та 0,12. Отримані значення занести до таблиці 1.3.
5. Визначити загальну похибку прямих вимірів, врахувавши її випадкову та систематичну складові. Для цього з табл. 1.1. визначити інструментальні похибки, записати їх у табл. 1.3. Якщо одна з цих похибок у 3 та більше разів більша за іншу, то меншою нехтуємо. Якщо ж ні – загальну похибку прямих вимірювань обчислити за формулою . Знайдені значення округлити за правилами п.4 і записати до таблиці 1.3.
6. Розрахувати за формулою (1.5) середнє значення густини в одиницях системи СІ.
7. Розрахувати за формулою (1.7) значення похибки непрямих вимірювань і округлити їх відповідно до правил, викладених у п.4.
8.
Округлити отримане значення густини
до розряду, що відповідає першій значущій
цифрі похибки і записати округлений
результат у вигляді
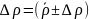 кг/м3.
кг/м3.


 мм
мм
 ,
г
,
г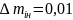
 г
г ,
г
,
г ,мм
,мм ,
мм
,
мм



