7. Формулы Байеса

Пусть событие В₁, В₂… В_n несовместны и образуют полную группу. Событие А может наступить при условии появления одного из них. В_i называем гипотезами.

Пусть произведено испытание и в результате появилось событие А. Тогда оказывается возможным определить условие вероятности гипотез Вi по следующим формулам:

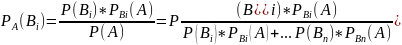
Эти формулы называются формулами Байеса. Они позволяют оценить вероятность гипотезы В_i во всех испытаниях, где наступает событие А. Иными словами, зная вероятность 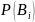, до проведения испытания мы можем переоценить ее после проведения испытания, в результате которого появилось событие А. Замечание! В данном случае справедлива формула P_A(В₁)+P_A(В₂)+…+P_A(B_n)=1

8.Формула Бернулли. Локальная теорема Лапласа. Формула Пуассона.

Если при проведении нескольких испытаний вероятность события А в каждом испытании не зависит от исходов других событий, то этих испытаниях называется независимыми относительно события А. Будем рассматривать только такие независимые испытания, в которых событие А имеет одинаковую вероятность. Пусть производится n независимых испытаний, в каждом из которых событие А может появиться с вероятностью Р, тогда вероятность противоположного события ( не наступления события А) также постоянно в каждом испытании и равна q =1-p. В тв представляет особый интерес случай, когда в n испытаниях событие А осуществляется k раз и не осуществляется n-k раз. Вероятность этого сложного события вычисляется по формуле Бернулли:

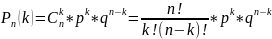
При очень больших значениях n т.е. когда число испытаний велико, формула Бернулли не применяется. В этом случае используют локальную теорему Лапласа.

Теорема: Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события А равна p (0 p 1), событие А наступит ровно k раз, приближенно равна 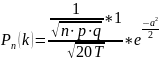, где .

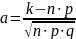Формула тем точнее, чем больше n.

При вычислении по этой формуле пользуются специальными таблицами для функции f(x)=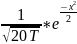 Таблица значений этой функции всегда приведена в приложении к учебнику. Эта функция четкая, т.е. f(-x)= f(x), поэтому в таблице обычно приводят её значения для положительных x. Тогда формулу для вероятностей можно записать в виде: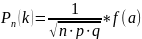 , где a= 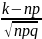. При больших значениях n и при малых значений вероятностей p вычисления по формуле Бернулли затруднительны. В Этомслучае используют формулу Пуассона: 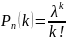, где λ=np .

9.Интегральная теорема Лапласа.

Предположим, что в каждом из произведенных n испытаниях событие А появляется с одинаковой вероятностью p , в прикладных вопросов теории вероятностей наиболее употребимы определение вероятности события А в n испытаниях, когда k изменяется в заданном интервале значений 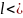k m , соответственная вероятность обозначается 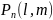. Формула для приближенного вычисления вероятностей устанавливается с помощью интегральной теоремы Лапласа.

Теорема: Пусть вероятность p наступления события А, в каждом испытании постоянно и 0<p<q, тогда вероятность того, что событие А появится в n испытаниях от 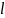до m раз вычисляется по формуле: 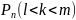= = 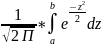, где

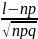а = , b=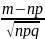

Формула 1:применима в случаях больших значениях n и k.При вычислениях по этой формуле пользуются специальными значениями таблиц для функции Лапласа.

Ф(x)= Таблица значений функции Ф(x) представлена в приложениях к учебнику. Эта функция нечетная, поэтому в таблице представлена значение для x>0, тогда для x<0 Ф(-x)= Ф(x). Формула 1 удобно использовать в виде формул Ньютона-Лейбница: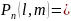 Ф(b)-Ф(a) , где а = , b=