1.Основные понятия теории вероятностей.

ТВ-наука о закономерностях случайных величин.

Под событием в ТВ понимается всякий факт,кот.может произойти или не произойти при осуществлении комплекса условий. Каждое такое осуществление наз-ся испытанием.

Достоверным наз-ся событие,которое обязательно произойдет при испытании.

Невозможным наз-ся событие,котрое заведомо не произойдет при испытании.

Случайным наз-я событие,которое в результате испытания может произойти/не произойти.

Предметом ТВ явл.вероятностные закономерности массовых случ.событий, где под массовостью понимается многократная повторяемость.

Комбинаторика-раздел матем.в котором изучаются задачи выбора элементов из заданного множества и расположение их в группы по заданным правилам.

Правило умножения: если элемент а можно выбирать м способами, а после каждого выбора элементов б можно выбирать н способами, то оба элемента а и б в указанном порядке можно выбрать м*н способами.

Замечание:это правило распр.на случай 3-х и более элементов.

Правило сложения: если элемент а можно выбрать м способами, а элемент б н способами, причем любой выбор элемента а отличен от любого выбора элемента б, то любой из указанных элементов а и б можно выбрать м+н способами.

Замечание: правило на случай 3-х и более элементов.

Размещение без повторений из н по м эл. наз-ют любой выбор м эл., взятых в опред.поряке из данных н эл.Причем один выбор от другого отличается либо составом эл.,либо порядком их расположения. А_n^m=n!/(n-m)!.

Размещение с повторением из н классов эл.по м эл.наз-ют любой выбор м эл., взятых в опред.порядке из данных н классов,при этом один и тот же эл.может повторяться в каждом размещении любое число раз. Причем один выбор от другого отличается либо составом эл.,либо порядком их расположения.А(ср.) _n^m=n^m.

Перестановками без повторений из н наз-ют размещения без повторений из н эл.по н.причем один выбор от другого отличается только порядком расположения.Р_n=n!

Перестановки с повторениями: из н классов эл.,по м эл.,наз-ют размещения с повторениями,состоящие из м эл.,среди которых от итого класса участвуют Китый элементов. Причем один выбор от другого отличается порядком расположения эл. Р_{к1*к2…кn}=(к1+к2+…кн)/к1!*к2!...кн!.

Сочетания без повторений из н эл.,по м эл,наз-ют размещение без повторений из н эл.,по м,отличающихся одно о другого хотя бы одним эл. Важен только состав.С_n^m=n!/m!(n-m)!.

Сочетания с повторениями из н классов эл, по м наз-ют такие размещения с повторениями из м классов эл,по м эл, котрое одно от другого отличается хотя бы одним эл. С(ср.) _n^m=(n+m-1)!/(n-1)!m!.

Свойства сочетаний:

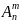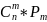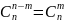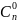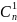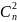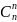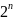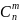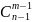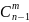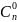1. = ;

2. ;

3. + + +… = ;

4. = + ;

5. = = 1;

2.Вероятность события.

События наз-ют несовметимыми, если в одном и том же испытании появление одного их них исключает появление другого.Несколько событий образуют полную группу, если в результате испытания появление хотя бы одного из них явл.достоверным событием.Назовемкаждый из возможных результатов испытания элементарным событием или исходом. Классич.определение вер-ти. Отношение числа м благопрепятствующих событию А элементарных исходов к общему числу н равновозможных несовместимых элементарных исходов,образующих полную группу наз-ся вер.событий А. Р(А)=м/н.м-кол-во благопр.исходов,н- общее кол-во исходов.

Св-ва вероятности:1. Вер-ть достов.события =1.

2.Вер-ть невозможного события=0.

3.Вер-ть случ.события есть положительная величина 0<Р(А) <1.Замеч.

Из свойств следует, что вер-ть любого события удовл.неравенству.(то же самое, только больше или равно).