4) Построение доверительной области для математического ожидания случайного вектора в форме прямоугольного параллелепипеда
Рассчитаем доверительную вероятность, с которой будем строить доверительные интервалы для математического ожидания каждого признака:
.
Для
построения доверительного интервала
для математического ожидания нормально
распределенной генеральной совокупности
при неизвестном среднем квадратическом
отклонении используется статистика
,
имеющая распределение Стьюдента с
числом степеней свободы
.
Решая уравнение
,
находим
– квантиль уровня
распределения Стьюдента с числом
степеней свободы
.
Доверительный интервал для m
имеет вид:
.
Значение
найдем с помощью функции Excel
СТЬЮДРАСПОБР(
),
где
.
Получим:
.
Оценки
средних квадратических отклонений
рассчитаны в пакете Statistica
(рисунок 2.4):
;
;
.
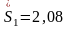С вероятностью 0,98 доверительные интервалы
для математического ожидания признаков
,
,
имею вид:
,
,
.
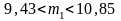Тогда с вероятностью 0,95 доверительная область для математического ожидания случайного вектора имеет вид прямоугольного параллелепипеда, изображенного на рисунке 2.13.
Рисунок 2.13 – Изображение доверительной области для вектора математических ожиданий в форме прямоугольного параллелепипеда
5) Проверка гипотезы о равенстве вектора математических ожиданий вектору
Проверим гипотезу о равенстве вектора
математических ожиданий
постоянному вектору
.
Выдвигаем гипотезы:
,
.
Так
как ковариационная матрица
не известна, то для проверки гипотезы
воспользуемся статистикой Хотеллинга
(2.5). Наблюдаемое значение статистики
вычислим с помощью пакета Mathcad.
Результаты вычислений представлены на
рисунке 2.14.
Рисунок 2.14 – Результаты расчета наблюдаемого значения статистики Хотеллинга при проверке гипотезы о значении вектора математических ожиданий
Критическую
точку найдем по формуле (2.6). С
помощью функции Excel
FРАСПОБР(
)
получаем, что
.
Тогда
.
Так
как
<
можно сделать вывод, что гипотеза
принимается, т.е. можно считать, что
математическое ожидание среднемесячного
объема продаж первого, второго и третьего
товаров составляется соответственно
10 тыс. руб., 20 тыс. руб. и 30 тыс. руб.
6) Проверка гипотезы об однородности распределения генеральных совокупностей и
Так
как генеральные совокупност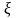и
и
распределены по нормальному закону, то
для проверки однородности их распределения
необходимо проверить, равны ли параметры
распределения, т.е. ковариационные
матрицы и вектора математических
ожиданий.
Проверим гипотезу о равенстве ковариационных матриц:
,
.
Оценка ковариационной матрицы генеральной совокупности составляет:
.
Наблюдаемое значение статистики W (2.7) рассчитано в пакете Mathcad, результаты представлены на рисунке 2.15.
Рисунок 2.15 – Результаты расчета наблюдаемого значения статистики при проверке гипотезы о равенстве ковариационных матриц
Критические
значения статистики W
найдем с помощью функции Excel
ХИ2ОБР(
;
),
которая выдает
-ую
точку распределения «Хи-квадрат» с
числом степеней свободы
:
(=ХИ2ОБР(0,975;6);
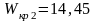(=ХИ2ОБР(0,025;6).
Так
как
не попало в критическую область
,
то гипотеза
принимается, т.е. ковариационные матрицы
генеральных совокупностей
и
равны.
Далее проверим гипотезу о равенстве векторов математических ожиданий генеральных совокупностей и :
;
.
Оценка
вектора математических ожиданий
генеральной совокупности
известна:
.
Наблюдаемое значение статистики
Хотеллинга (2.8) рассчитаем в пакете
Mathcad
(рисунок 2.16).
Рисунок 2.16 – Результаты расчета наблюдаемого значения статистики при проверке гипотезы о равенстве математических ожиданий
С
помощью функции FРАСПОБР(
)
пакета Exсel
найдем
-ую
точку распределения Фишера-Снедекора
с числом степеней свободы
,
:
.
По формуле (2.9) рассчитаем критическое
значение статистики
:
.
Так
как
,
то гипотеза
о равенстве векторов математических
ожиданий
и
принимается. Таким образом, генеральные
совокупности
и
однородны. Это означает, что нет различий
в среднемесячном объеме продаж товаров
1, 2, 3 в городах «А» и «Б», что дает
возможность объединить выборки из
генеральных совокупностей
и
в одну, объем которой составит 90 торговых
точек.