2.8 Задание, порядок выполнения и вопросы к защите лабораторной работы на тему «Оценивание параметров распределения и проверка гипотез о параметрах распределения многомерной генеральной совокупности»

Задание к лабораторной работе

По выборочным данным о среднемесячном объеме продаж трех товаров в 50 торговых точках города «А», представленным в таблице А.1, осуществить оценивание параметров и проверку гипотез о параметрах нормально распределенного случайного вектора , где – среднемесячный объем продаж товара 1 (тыс. руб.), – среднемесячный объем продаж товара 2 (тыс. руб.), – среднемесячный объем продаж товара 3 (тыс. руб.). Для этого:

1. найти оценки параметров распределения случайного вектора ;

2. с вероятностью 0,95 построить доверительную область для математического ожидания случайного вектора в форме эллипсоида;

3. с вероятностью 0,95 построить доверительную область для математического ожидания случайного вектора при нивелировании признака ;

4. с вероятностью 0,95 построить доверительную область для математического ожидания случайного вектора в форме прямоугольного параллелепипеда;

5. на уровне значимости проверить гипотезу о равенстве вектора математических ожиданий вектору , значение которого приведено в таблице А.2;

6. на уровне значимости проверить гипотезу об однородности распределения генеральных совокупностей и , где – среднемесячный объем продаж (тыс. руб.) товара 1, 2, 3 соответственно в городе «Б», параметры и не известны, однако по данным 40 торговых точек города «Б» вычислены значение оценок параметров, приведенные в таблице А.2.

Порядок выполнения лабораторной работы

Лабораторная работа выполнена по данным нулевого варианта таблиц А.1, А.2, А.3 с помощь пакетов Statistica, Mathcad.

1) Нахождение оценок параметров распределения случайного вектора

Так как случайный вектор ), то необходимо рассчитать оценку вектора математических ожиданий и оценку ковариационной матрицы .

Оценкой вектора математических ожиданий является вектор средних арифметических . Для расчета вектора средних арифметических 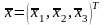воспользуемся пакетом Statistica. Для этого после ввода исходных данных необходимо выбрать пункты меню «Statistics», «Basic Statistics/Tables» (рисунок 2.1). В появившейся форме, представленной на рисунке 2.2, выбрать «Descriptive statistics» и нажать кнопку «ОК». В появившейся форме «Descriptive statistics» нажать кнопку «Variables» и в появившемся окне, представленном на рисунке 2.3, выбрать три первых признака (1-3) и нажать «ОК». Для получения результатов расчета нажать кнопку «Summary». Среднее арифметическое значение каждого признака представлено в столбце «Mean» таблицы, представленной на рисунке 2.4.

Рисунок 2.1 – Выбор пунктов меню для расчета средних арифметических значений признаков

Рисунок 2.2 – Вид формы «Basic Statistics and Tables»

Рисунок 2.3 – Окно выбора признаков для анализа в форме «Descriptive Statistics»

Рисунок 2.4 – Результаты расчета средних значений признаков

Получили , т.е. средние значения среднемесячного объема продаж первого, второго и третьего товаров составляют соответственно 10,14 тыс. руб., 20,22 тыс. руб., 29,87 тыс. руб.

Для расчета смещенной и несмещенной оценок ковариационной матрицы по формулам и воспользуемся пакетом Mathcad. Порядок расчетов представлен на рисунке 2.5.

Рисунок 2.5 – Расчет оценки ковариационной матрицы в пакете Mathcad

Таким образом, получили:

, .