Механика жидкостей и газов

Первый закон Фика – масса вещества, перенесенная за время ∆t при диффузии

,

где – градиент плотности в направлении, перпендикулярном к площадке , – коэффициент диффузии ( – средняя арифметическая скорость, – средняя длина свободного пробега молекул).

Импульс, перенесенный газом за время , определяет силу внутреннего трения F_тр в газе:

,

где – градиент скорости течения газа в направлении, перпендикулярном к площадке , – динамическая вязкость. .

Формула Стокса (сила сопротивления движению шарика радиусом r со скоростью )

.

Уравнение Бернулли:

,

где – динамическое давление, – статическое давление. [p] = Па (паскаль) = Н/м².

Количество теплоты, перенесенное за время вследствие теплопроводности, определяется формулой

,

где – градиент температуры в направлении, перпендикулярном к площадке , – коэффициент теплопроводности.

Первое начало термодинамики

,

где – количество теплоты, полученное телом, – изменение внутренней энергии , – работа, совершаемая телом при изменении его объема. Полная работа объема газа

.

Уравнение теплового баланса (без учета теплопотерь сумма теплот , отданное холодным телам, равно сумме теплот , принятой этими телами)

.

Работа, совершаемая при изотермическом изменении объема газа

.

Давление газа и его объем связаны при адиабатическом процессе уравнением Пуассона

, ,

где показатель адиабаты . Уравнение Пуассона может быть записано еще в таком виде: ,

или , т.е. .

Работа, совершаемая при адиабатическом изменении объема газа

,

где р₁ и V₁ – давление и объем газа при температуре Т₁.

Коэффициент полезного действия (КПД) тепловой машины

,

где – количество теплоты, полученное рабочим телом от нагревателя, – количество теплоты, отданное холодильнику. Для идеального цикла Карно

,

где и Т₂ – термодинамические температуры нагревателя и холодильника.

Энтропия – термодинамическая функция, выражающая состояние системы и степень беспорядка в ней

,

где k – постоянная Больцмана, W – вероятность состояния системы.

Разность энтропии двух состояний 2 и 1 определяется формулой

.

Изменение энтропии (∆S) при нагревании тела от температуры Т₁ до Т₂:

.

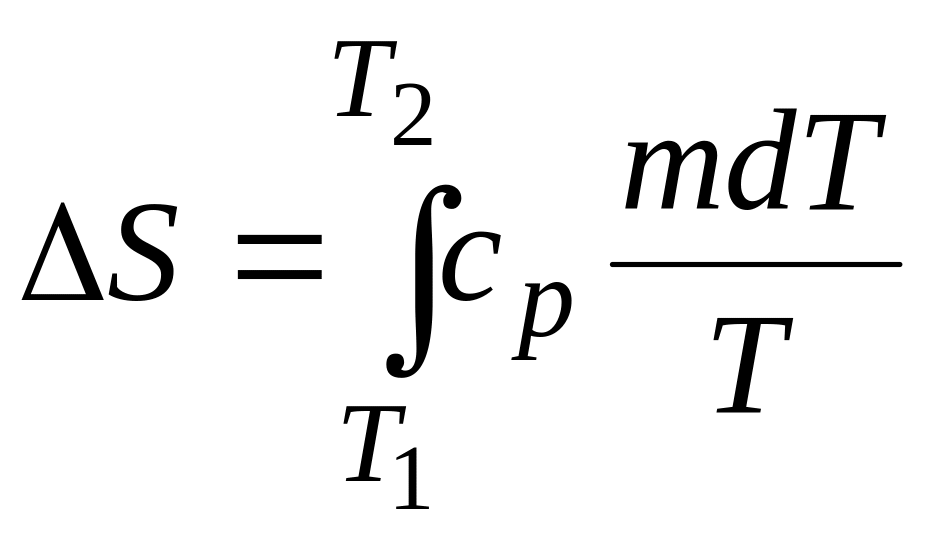Второе начало термодинамики – энтропия изолированной системы не может убывать

.

С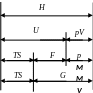 вязь между основными термодинамическими функциями и параметрами

Н = U + рV,

U = F + ТS,

G = F + рV,

где Н – энтальпия; U – внутренняя энергия; G – свободная энергия Гиббса; F – свободная энергия

Гельмгольца, ТS и рV – связанные энергии, вносящие вклад в различные превращения в системе (фазовые превращения, химические реакции, адиабатные явления и др.).

Фазовыми переходами I рода называются такие превращения, при которых скачком меняется первая производная от термодинамической функции.

; ;

; .

Под фазовыми переходами I рода понимают фазовые превращения, сопровождающиеся поглощением или выделением скрытой теплоты и скачкообразным изменением удельного объема V  0 и энтропии S  0.

К фазовым переходам I рода относятся кристаллизация, плавление, парообразование, конденсация, полиморфные переходы и пр.

Основным уравнением, характеризующим фазовые переходы I рода, является уравнение Клапейрона-Клаузиуса

,

где и – объемы одной и второй фаз.

Зависимость температуры фазовых превращений от давления:

.

Плавление – это превращение кристаллического тела в жидкое состояние при температуре плавления Т_L.

Теплота плавления

Q = Lm,

где L – удельная теплота плавления, m – масса тела.

Кристаллизация – это процесс перехода вещества из жидкого состояния в твердое кристаллическое при охлаждении.

Полиморфизм – свойство одного и того же вещества пребывать при определенных условиях в разных кристаллографических модификациях.

Полиморфные превращения – это переход одной фазы твердого вещества в другую фазу того же вещества.

Теплота кипения (парообразования)

,

где r – удельная теплота парообразования.

Теплота сгорания топлива

,

где q – удельная теплота сгорания топлива.

Изменение энтропии при фазовом превращении

или ,

где Q, – теплота и энтальпия фазового превращения, – температура фазового превращения.

Изменение энергии Гиббса системы при нагревании тела, при постоянном давлении

,

где , – начальная температура тела, – изменение энтальпии.

Изменение энергии Гиббса при кристаллизации переохлажденной жидкости, при постоянном давлении

,

где ( ) – переохлаждение, – температура плавления, – энтальпия плавления.

Минимальный размер кристаллика l_k и работа его образования A_k из переохлажденной жидкости при кристаллизации. Для кристаллика кубической формы

, ,

где – переохлаждение, – температура плавления, – удельная теплота плавления, – плотность, – межфазное поверхностное натяжение.

Скорость массовой кристаллизации жидкой фазы

.

Линейная скорость затвердевания жидкой фазы

,

где – коэффициент теплопроводности, – площадь растущей поверхности, – градиент температуры.

Фазой называется часть системы, которая имеет границу раздела и может быть отделена от общей системы механическим путем. Число фаз обозначают буквой Ф. Фазами могут считаться газообразное, жидкое, твердое состояния и др. Так, в системе лёд-вода при 0С имеются две фазы (Ф = 2).

Компонент – независимая часть системы, имеющая свою химическую формулу, т.е. компонент – это индивидуальное вещество. Числе компонентов обозначается буквой К в системе, например, лед-вода К = 1, компонентом является химическое соединение , а число фаз Ф = 2.

Термодинамическая степень свободы системы определяется числом независимых переменных (давление – р, температура – Т, концентрация – С и т.д.), которые можно изменять в определенных пределах, не нарушая равновесия. Чисто степеней свободы обозначается буквой i.

Закономерности всех изменений системы в зависимости от внутренних и внешних условий подчиняются правилу фаз Гиббса

,

где В – число внешних воздействий (температура, давление и т.д.).

Обычно для простых веществ, сплавов и растворов принимают два внешних фактора: температуру и давление. В этом случае В = 2, а правило фаз Гиббса пишут в виде

.

Если же за внешний фактор принять один из этих параметров (либо температуру, либо давление), тогда В = 1:

.

Например, в системе лед-вода при атмосферном давлении и при температуре 0°С:

,

т.е. система такая существует, но она не имеет степеней свободы.

Если система называется нонвариантной, если – моновариантной, если – бивариантной. При система существовать не может.

С учетом химических реакций между компонентами системы число независимых компонентов уменьшается в зависимости от числа уравнений У, с помощью которых можно связать концентрации веществ. В этом случае правило фаз будет иметь вид:

І = – Ф + В,

где = К – У.

Сплавами называют твердые вещества, полученные путем расплавления двух или нескольких компонентов и последующей кристаллизации.

По характеру взаимодействия компонентов различают такие сплавы как твердые растворы, механические смеси и химические соединения.

Диаграмма состояния – это график зависимости температуры плавления и кристаллизации сплава в зависимости от состава.

Концентрация – величина, определяющая содержание компонента в смеси, растворе, сплаве. Способы выражения концентрации различны.

Относительная массовая концентрация – отношение массы компонента m_i к общей массе смеси

.