Контрольная работа 1 теоретические вопросы

0. 1.1. Кинематика материальной точки. Материальная точка. Система отсчета. Число степеней свободы. Траектория. Путь. Перемещение. Размерности физических величин. Скорость. Единицы измерения скорости. Мгновенная скорость. Средняя скорость. Прямолинейное равномерное движение. Относительность движения. Графики пути и скорости при прямолинейном равномерном движении.

1. 1.2. Ускорение. Ускорение при прямолинейном движении. Уравнение равнопеременного движения. Формулы пути и скорости при равнопеременном движении. Ускорение свободного падения. Движение тела, брошенного вертикально вверх, вниз. Графики равнопеременных движений.

2. 1.3. Криволинейное движение. Нормальное и тангенциальное составляющие ускорения при криволинейном движении. Общее ускорение при криволинейном движении. Классификация движений при анализе ускорений. Движение тела, брошенного горизонтально и под углом к горизонту.

3. 1.4. Вращательное движение материальной точки. Равномерное движение по окружности. Линейная и угловая скорости при вращательном движении. Радианная мера угла. Период и частота вращения. Связь угловой скорости с периодом и частотой вращения. Единицы измерения угловой скорости, периода и частоты. Центростремительное ускорение.

4. 1.5. Угловое ускорение. Единицы измерения угловой скорости и углового ускорения. Направление вектора углового ускорения. Основное уравнение кинематики вращательного движения. Связь линейных и угловых величин.

5. 1.6. Динамика. Инерциальные и неинерциальные системы отсчета. Инерция. Первый закон Ньютона – закон инерции. Масса тела. Сила. Единицы измерения. Инертная и гравитационная масса. Второй закон Ньютона. Третий закон Ньютона. Принцип независимости действия сил.

6. 1.7. Силы в механике. Сила упругости. Закон Гука (для пружины). Сила реакции опоры. Сила натяжения нити. Физическая природа силы упругости. Сила трения. Трение покоя. Трение качения. Трение скольжения. Закон всемирного тяготения. Гравитационная постоянная. Центростремительная сила. Движение тела под действием нескольких сил (примеры).

7. 1.8. Импульс тела. Замкнутая система. Главный вектор внешних сил. Центр масс. Основное уравнение динамики поступательного движения. Уравнение движения тела переменной массы. Закон сохранения импульса тела. Реактивное движение (примеры). Упругие и неупругие соударения (примеры). Центральный удар.

8. 1.9. Механическая работа. Элементарная и интегральная работа. Единицы измерения работы. Консервативные и диссипативные силы. Работа силы упругости. Работа силы тяжести. Работа силы трения. Мощность. Единицы измерения мощности.

9. 1.10. Механическая энергия. Кинетическая и потенциальная энергия. Полная механическая энергия. Связь работы и энергии. Энергия как функция состояния системы. Понятие о градиенте скалярной функции координат. Закон сохранения механической энергии. Примеры. Всеобщий закон сохранения энергии. Коэффициент полезного действия (КПД).

10. 1.11. Динамика вращательного движения. Абсолютно твердое тело. Движение твердого тела. Движение центра инерции твердого тела. Вращение твердого тела. Момент силы. Направление момента силы относительно оси вращения. Момент пары сил. Правило моментов (примеры).

11. 1.12. Статика. Элементы статики. Сложение и разложение сил. Равнодействующие и уравновешивающие силы. Точка приложение силы. Равновесие тел, имеющих ось вращения. Равновесие тел, не имеющих оси вращения. Примеры.

12. 1.13. Момент инерции. Момент инерции тела относительно оси вращения. Единицы измерения момента инерции. Вычисление момента инерции однородного сплошного цилиндра. Примеры значений момента инерции для тел различной формы. Теорема Штейнера.

13. 1.14. Работа и энергия при вращательном движении твердого тела. Кинетическая энергия тела вращения. Полная энергия тела, совершающего одновременно поступательное и вращательное движение. Основное уравнение динамики вращательного движения.

14. 1.15. Момент импульса. Направление момента импульса тела относительно оси вращения. Связь момента импульса с моментом инерции и угловой скоростью вращения. Основное уравнение динамики вращательного движения тела относительно оси. Закон сохранения момента импульса. Свободные оси. Гироскоп. Прецессия.

15. 1.16. Гидростатика и аэростатика. Сплошные среды. Несжимаемая жидкость. Давление. Единицы измерения давления. Атмосферное давление. Барометры. Закон Паскаля. Давление жидкости на дно и стенки сосуда. Закон Архимеда. Определение плотностей жидких и твердых тел гидростатическим взвешиванием (вывод формулы).

16. 1.17. Элементы гидродинамики. Течение. Поток. Линии тока. Трубка тока. Ламинарное и турбулентное течение. Уравнение неразрывности струи. Идеальная жидкость. Уравнение Бернулли (вывод). Статическое, динамическое и гидростатическое давление. Манометры. Водоструйный насос. Реальные жидкости.

17. 1.18. Механические колебания. Свободные гармонические колебания и их характеристики. Математический маятник. Уравнение свободных незатухающих колебаний математического маятника. Амплитуда, период, частота и фаза колебаний. Единица измерения частоты колебаний.

18. 1.19. Физический маятник. Пружинный маятник. Уравнение свободных незатухающих колебаний физического маятника и колебаний тела на пружине. График координаты при незатухающих колебаниях.

19. 1.20. Скорость и ускорение при гармоническом колебательном движении. Вывод уравнений. Графики ускорения при колебательном движении. Энергия гармонических колебаний.

20. 1.21. Сложение гармонических колебаний. Сложение колебаний вдоль одной прямой. Вывод уравнения. Биение. Сложение двух взаимно перпендикулярных колебаний. Вывод уравнения. Фигуры Лисажу.

21. 1.22. Затухающие механические колебания. Уравнения затухающих колебаний и его решение. Амплитуда затухающих колебаний. Логарифмический декремент затухания и коэффициент затухания. Автоколебания.

22. 1.23. Вынужденные механические колебания. Дифференциальное уравнение вынужденных колебаний и его решение. Резонанс колебаний. Резонансные явления в технике.

23. 1.24. Механические волны. Длина волны. Скорость распространения волны. Виды волн (продольные, поперечные, плоские, сферические). Фронт волны. Луч. Принцип Гюйгенса. Уравнение бегущей волны. Интерференция волн. Стоячие волны. Групповая скорость. Волновой пакет. Плотность потока. Вектор Умова.

24. 1.25. Акустика. Звук. Ультразвук. Инфразвук. Энергия звуковой волны. Плотность энергии. Поток звуковой энергии. Интенсивность звука. Громкость звука. Высота звука. Шум. Уровень громкости. Скорость звука в различных средах. Эффект Доплера.

ЗАДАЧИ

1.1. Тело брошено вертикально вверх с начальной скоростью  м/с. Когда оно достигло верхней точки полета из того же начального пункта, с той же скоростью  м/с вертикально вверх было брошено второе тело. На каком расстоянии h от начального пункта встретятся тела? Сопротивлением воздуха пренебречь. 

1.2. Материальная точка движется прямолинейно с ускорением . Определить, на сколько путь, пройденный точкой в n–ю секунду, больше пути, пройденного в предыдущую секунду. Принять = 0. 

1.3. Две автомашины движутся по дорогам, угол между которыми 60. Скорость автомашин  км/ч и  км/ч. С какой скоростью удаляются машины одна от другой? 

1.4. Эскалатор метро поднимает неподвижно стоящего на нем пассажира в течение 1 мин. По неподвижному эскалатору пассажир поднимается за 3 мин. Сколько времени будет подниматься идущий вверх пассажир по движущемуся эскалатору?

1.5. Легковой автомобиль движется со скоростью 20 м/с за грузовым, скорость которого 16.5 м/с. В момент начала обгона водитель легкового автомобиля увидел встречный междугородный автобус, движущийся со скоростью 25 м/с. При каком наименьшем расстоянии до автобуса можно начинать обгон, если в начале обгона легковая машина была в 15 м от грузовой, а к концу обгона она должна быть впереди грузовой на 20 м?

1.6. Катер, переправляясь через реку, движется перпендикулярно течению реки со скоростью 4 м/с в системе отсчета, связанной с водой. На сколько метров будет снесен катер течением, если ширина реки 800 м, а скорость течения 1 м/с?

1.7. Велосипедист ехал из одного пункта в другой. Первую треть пути он проехал со скоростью = 18 км/ч. Далее половину оставшегося времени он ехал со скоростью = 22 км/ч, после чего до конечного пункта он шел пешком со скоростью = 5 км/ч. Определить среднюю скорость велосипедиста. 

1.8. Во сколько раз скорость пули в середине ствола ружья меньше, чем при вылете из ствола?

1.9. Уклон горы длиной 100 м лыжник прошел за 20 с, двигаясь с ускорением 0.3 м/с². Какова скорость лыжника в начале и в конце уклона?

1.10. Поезд, двигаясь под уклон, прошел за 20 с путь 340 м и развил скорость 19 м/с. С каким ускорением двигался поезд и какой была скорость в начале уклона?

1.11. Движения двух автомобилей по шоссе заданы уравнениями и . Описать картину движения. Найти: а) время и место встречи автомобилей; б) расстояние между ними через 5 с от начала отсчета времени; в) координату первого автомобиля в тот момент времени, когда второй находился в начале отсчета.

1.12. Материальная точка движется в плоскости ху согласно уравнениям и , где b₁ = 7 м/с, с₁ = –2 м/с², в₂ = –1 м/с, с₂ = 0.2 м/с². Найти модули скорости и ускорения в момент времени t = 5 с. 

1.13. Поезд, идя по горизонтальному пути со скоростью 36 км/ч, переходит на равноускоренное движение и проходит 600 м, имея в конце пути скорость 45 км/ч. Определить ускорение и время ускоренного движения. Построить график зависимости скорости от времени.

1.14. Тело брошено под углом 30 к горизонту со скоростью = 30 м/с. Каковы будут нормальное a_n и тангенциальное a_τ ускорения тела через время t = 1 c после начала движения? 

1.15. Минутная стрелка часов в 3 раза длиннее секундной. Найти отношение скоростей концов стрелок.

1.16. Пловец, спрыгнув с пятиметровой вышки, погрузился в воду на глубину 2 м. Сколько времени и с каким ускорением он двигался в воде?

1.17. Сколько времени падало тело, если за последние 2 с оно прошло 60 м?

1.18. Тело брошено вертикально вверх со скоростью 30 м/с. На какой высоте и через сколько времени скорость тела (по модулю) будет в три раза меньше, чем в начале подъема?

1.19. Мальчик бросил горизонтально мяч из окна, находящегося на высоте 20 м. Сколько времени летел мяч до земли, и с какой скоростью он был брошен, если он упал на расстоянии 6 м от основания дома?

1.20. Дальность полета тела, брошенного в горизонтальном направлении со скоростью = 10 м/с, равна высоте бросания. С какой высоты h брошено тело?

1.21. Снаряд, вылетевший из орудия под углом к горизонту, находился в полете 12 с. Какой наибольшей высоты достиг снаряд?

1.22. С балкона, расположенного на высоте 20 м, бросили мяч под углом 30° вверх от горизонта со скоростью 10 м/с. Направив ось x вдоль поверхности земли вправо, а ось y вдоль стены дома вверх, написать уравнения зависимости координат от времени х = x(t) и у = y(t) и уравнение траектория у = у(х). Найти: а) координаты мяча через 2 с; б) через какой промежуток времени мяч упадет на землю; в) горизонтальную дальность полета.

1.23. По краю равномерно вращающейся с угловой скоростью платформы идет человек и обходит платформу за время t = 9.9 с. Каково наибольшее ускорение а движения человека относительно Земли? Принять радиус платформы R = 2 м. 

1.24. С тележки, свободно движущейся по горизонтальному пути со скоростью = 3 м/с в сторону, противоположную движению тележки, прыгает человек, после чего скорость тележки изменилась и стала равной u₁ = 4м/с. Определить горизонтальную составляющую скорости u_2x человека при прыжке относительно тележки. Масса тележки m₁ = 210 кг, масса человека m₂ = 70 кг. 

1.25. Орудие, жестко закрепленное на железнодорожной платформе, производит выстрел под углом 30 к линии горизонта. Определить скорость u₂ отката платформы, если снаряд вылетает со скоростью u₁ = 480 м/с. Масса платформы с орудием и снарядами m₂ = 18 т, масса снаряда m₁ = 60 кг. 

1.26. Конькобежец, стоя на коньках на льду, бросает камень массой m₁ = 2.5 кг под углом 30 к горизонту со скоростью  = 10 м/с. Какова будет начальная скорость движения конькобежца, если масса его m₂ = 60 кг? Перемещением конькобежца во время броска пренебречь. 

1.27. Снаряд, летевший со скоростью  = 400 м/с, в верхней точке траектории разорвался на два осколка. Меньший осколок, масса которого составляет 40% от массы снаряда, полетел в противоположном направлении со скоростью u₁ = 150 м/с. Определить скорость u₂ большего осколка. 

1.28. В деревянный шар массой m₁ = 8 кг, подвешенный на нити длиной l = 1.8 м, попадает горизонтально летящая пуля массой m₂ = 4 г. С какой скоростью летела пуля, если нить с шаром и застрявшей в нем пулей отклонилась от вертикали на угол 3. Размером шара пренебречь. Удар пули считать прямым, центральным. 

1.29. По небольшому куску мягкого железа, лежащему на наковальне массой m₁ = 300 кг, ударяет молот массой m₂ = 8 кг. Определить КПД удара, если удар неупругий. Полезной считать энергию, затраченную на деформацию куска железа. 

1.30. Шар массой m₁ = 1 кг движется со скоростью = 4 м/c и сталкивается с шаром массой m₂ = 2 кг, движущимся навстречу ему со скоростью = 3 м/с. Каковы скорости u₁ и u₂ шаров после удара? Удар считать абсолютно упругим, прямым, центральным. 

1.31. Шар массой m₁ = 3 кг движется со скоростью = 2 м/c и сталкивается с покоящимся шаром массой m₂ = 5 кг. Какая работа будет совершена при деформации шаров? Удар считать абсолютно неупругим, прямым и центральным. 

1.32. Два шара массами m₁ = 6 кг и m₂ = 4 кг сталкиваются со скоростями = 8 м/c и = 3 м/с и после неупругого удара движутся как единое целое. Определить скорость шаров после удара, если до удара они двигались вдоль одной прямой в одну сторону; в противоположные стороны под углом 60.

1.33. Стоящий на льду человек массой m₁ = 60 кг ловит мяч массой m₂ = 0.5 кг, который летит горизонтально со скоростью = 20 м/с. На какое расстояние откатится человек с мячом по горизонтальной поверхности льда, если коэффициент трения = 0.05?

1.34. Спортсмен массой 65 кг, прыгая с десятиметровой вышки, входит в воду со скоростью 13 м/с. Найти среднюю силу сопротивления воздуха.

1.35. Поезд массой 3000 т движется вниз под уклон, равный 0.003. Коэффициент сопротивления движению равен 0.008. С каким ускорением движется поезд, если сила тяги локомотива равна: а) 300 кН; б) 150 кН; в) 90 кН?

1.36. С каким ускорением а скользит брусок по наклонной плоскости с углом наклона 30° при коэффициенте трения = 0.2.

1.37. Автомобиль массой 2 т проходит по выпуклому мосту, имеющему радиус кривизны 40 м, со скоростью 36 км/ч. С какой силой автомобиль давит на мост в его середине?

1.38. С какой максимальной скоростью может ехать мотоциклист по горизонтальной плоскости, описывая дугу радиусом 100 м, если коэффициент трения резины о почву 0.4? На какой угол от вертикального положения он при этом отклоняется?

1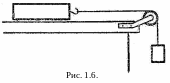 .39. Брусок массой 400 г под действием груза массой 100 г (рис. 1.6) проходит из состояния покоя путь 80 см за 2 с. Найти коэффициент трения.

1.40. На шнуре, перекинутом через неподвижный блок, помещены грузы массами 0.3 кг и 0.2 кг. С каким ускорением движутся грузы? Какова сила натяжения шнура во время движения?

1.41. Движение материальной точки описывается уравнением х = 5 – 8t + 4t². Приняв ее массу равной 2 кг, найти импульс через 2 с и через 4 с после начала отсчета времени, а также силу, вызвавшую это изменение импульса.

1.42. С судна массой 750 т произведен выстрел из пушки в сторону, противоположную его движению, под углом 60° к горизонту. На сколько изменилась скорость судна, если снаряд массой 30 кг вылетел со скоростью 1 км/с относительно судна?

1.43. Из шахты глубиной h = 600 м поднимают клеть массой m₁ = 3.0 т на канате, каждый метр которого имеет массу m = 1.5 кг. Какая работа А совершается при поднятии клети на поверхность Земли? Каков коэффициент полезного действия подъемного устройства?

1.44. Пружина жесткостью k = 500 H/м сжата силой F = 100 H. Определить работу А внешней силы, дополнительно сжимающей пружину ещё на ∆l = 2 см.

1.45. Из пружинного пистолета с пружиной жесткостью k = 150 Н/м был произведен выстрел пулей массой m = 8 г. Определить скорость пули при вылете её из пистолета, если пружина была сжата на ∆х =  4 см. 

1.46. Какая работа А должна быть совершена при поднятии с земли материалов для постройки цилиндрической дымоходной трубы высотой h = 40 м, наружным диаметром d₁ = 3 м и внутренним диаметром d₂ = 2 м? Плотность материала принять равной 2.8·10³ кг/м³.

1.47. По касательной к шкиву маховика в виде диска диаметром d = 75 см и массой m = 40 кг приложена сила F = 1 кН. Определить угловое ускорение и частоту вращения маховика через время t = 10 c после начала действия силы, если радиус r шкива равен 12 см. Силой трения пренебречь. 

1.48. На обод маховика диаметром d = 60 см намотан шнур, к концу которого привязан груз массой m = 2 кг. Определить момент инерции J маховика, если он, вращаясь равноускоренно под действием силы тяжести груза, за время t = 3 c приобрел угловую скорость = 9 рад/с. 

1.49. Нить с привязанными к её концам грузами массами m₁ = 50 г и m₂ = 60 г перекинута через блок диаметром d =4 см. Определить момент инерции J блока, если под действием силы тяжести грузов он получил угловое ускорение  = 1.5 рад/c². Трением и проскальзыванием нити по блоку пренебречь. 

1.50. Стержень вращается вокруг оси, проходящей через его середину, согласно уравнению , где А = 2 рад/с, В = 0.2 рад/с³. Определить вращающий момент М, действующий на стержень через время t = 2 c после начала вращения, если момент инерции стержня J = 0.048 кг·м². 

1.51. Блок, имеющий форму диска массой m = 0.4 кг, вращается под действием силы натяжения нити, к концам которой подвешены грузы массами m₁ = 0.3 кг, m₂ = 0.7 кг. Определить силы натяжения Т₁ и Т₂ нити по обе стороны блока.

1.52. К концам лёгкой и нерастяжимой нити, перекинутой через блок, подвешены грузы массами m₁ = 0.2 кг и m₂ = 0.3 кг. Во сколько раз отличаются силы, действующие на нить по обе стороны от блока, если масса блока m = 0.4 кг, а его ось движется вертикально вверх с ускорением a = 2 м/с²? Силами трения и проскальзывания нити по блоку пренебречь. 

1.53. Платформа в виде диска диаметром d = 3 м и массой m₁ = 180 кг может вращаться вокруг вертикальной оси. С какой угловой скоростью будет вращаться эта платформа, если по её краю пойдет человек массой m₂ = 70 кг со скоростью  = 1.8 м/с относительно платформы? 

1.54. Однородный стержень длиной l = 1.0 м может свободно вращаться вокруг горизонтальной оси, проходящей через один из его концов. В другой конец абсолютно неупруго ударяет пуля массой m₁ = 7 г, летящая перпендикулярно стержню и его оси. Определить массу m₂ стержня, если в результате попадания пули он отклонится на угол  = 60°. Принять скорость пули  = 360 м/с. 

1.55. С поверхности Земли вертикально вверх пущена ракета со скоростью  = 5 км/с. На какую высоту она поднимется? 

1.56. Какую скорость должен иметь искусственный спутник, чтобы обращаться по круговой орбите на высоте 600 км над поверхностью Земли? Каков период его обращения?

1.57. По круговой орбите вокруг Земли обращается спутник с периодом Т = 90 мин. Определить высоту спутника. Ускорение свободного падения у поверхности Земли и её радиус R считать известными. 

1.58. Груз массой 60 кг подвешен на кронштейне АВС (рис. 1.7). Угол между горизонтальным стержнем АВ и подкосом ВС равен 60. Определить усилие, сжимающее подкос ВС и растягивающее стержень АВ.

1.59. На кронштейне АВС (рис. 1.8), горизонтальная поперечина которого равна 48 см, а подкос 80 см, висит груз 12 кг. Определить действие веса груза на составляющие кронштейна.

1.60. Уличный фонарь массой 20 кг висит на двух стержнях, прикрепленных к стене дома на расстоянии 60 см друг от друга (рис. 1.9). Длина стержня АС равна 90 см, ВС = 120 см. Определить силу, растягивающую стержень АС и сжимающую стержень ВС.

1.61. Груз 60 кг висит на двух тросах, причем угол АСВ = 120 (рис. 1.10). Определить силы, растягивающие тросы АС и ВС.

1.62. Нить с шаром массой 50 г отклонена от положения равновесия на угол 30. Найти силу, стремящуюся возвратить шарик в положение равновесия и силу натяжения нити.

1.63. Две параллельные силы 20 Н и 30 Н приложены к концам твердого стержня длиной 1.5 м. Определить величину равнодействующей силы и точку ее приложения.

1.64. На балке, лежащей на двух опорах А и В, необходимо подвесить груз 14000 Н. Длина балки 7 м. Где следует подвесить данный груз, чтобы на опору А он давил с силой 5000 Н?

Рис. 1.7.	Рис. 1.8.
Рис. 1.9.	Рис. 1.10.

1.65. Концы балки, длина которой 10 м и масса 10 т, лежат на двух опорах. На расстоянии 2 м от левого конца на балке лежит груз массой 5 т. Определить силы реакции опор.

1.66. К стержню длиной 120 м приложены три параллельные силы одинакового направления: у левого конца стержня 30 Н, в середине 80 Н и у правого конца 90 Н. Чему равна равнодействующая этих сил? Где лежит точка ее приложения?

1.67. В воде с глубины 5 м поднимают до поверхности камень объемом 0,6 м³. Плотность камня 2500 кг/м³. Найти работу по подъему камня.

1.68. Какую работу надо совершить, чтобы лежащий на земле однородный стержень длиной 2 м и массой 100 кг поставить вертикально?

1.69. Какую работу надо совершить, чтобы по плоскости с углом наклона 30° втащить груз массой 400 кг, прикладывая силу, совпадающую по направлению с перемещением, на высоту 2 м при коэффициенте трения 0.3? Каков при этом КПД?

1.70. Насос, двигатель которого развивает мощность 25 кВт, поднимает 100 м³ нефти на высоту 6 м за 8 мин. Найти КПД установки.

1.71. Скорость течения воды в широкой части трубы 10 см/с. Какова скорость ее течения в узкой части, диаметр которой в 4 раза меньше диаметра широкой части?

1.72. Малый поршень гидравлического пресса за один ход опускается на 25 см, а большой поднимается на 5 мм. Определить силу давления, передаваемую на большой поршень, если на малый поршень действует сила 198 Н.

1.73. Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, уравнения которых и , где А₁ = 8 см, А₂ = 4 см, с^–1. Написать уравнение траектории и построить её. Показать направление движения точки. 

1.74. Точка совершает простые гармонические колебания, уравнения которых , где А = 5 см,  с^–1. В момент времени, когда точка обладала потенциальной энергией W_p = 0.1 мДж, на неё действовала возвращающая сила F = 5 мН. Найти этот момент времени.

1.75. Определить частоту простых гармонических колебаний диска радиусом R = 20 см около горизонтальной оси, проходящей через середину радиуса диска перпендикулярно его плоскости.

1.76. Найти логарифмический декремент затухания математического маятника, если за 1 мин амплитуда колебаний уменьшилась в 2 раза. Длина маятника 1 м.

1.77. Материальная точка совершает простые гармонические колебания так, что в начальный момент времени смещение х₀ = 4 см, а скорость = 10 см/с. Определить амплитуду А и начальную фазу колебаний, если их период Т = 2 с. 

1.78. Складываются два колебания одинакового направления и одинакового периода: и , где А₁ = А₂ = 3 см,  с^–1,  с. Определить амплитуду А и начальную фазу результирующего колебаний. Написать его уравнение. Построить векторную диаграмму для момента времени t = 0.