
- •Предисловие
- •Общие методические указания
- •Основные единицы международной системы (си) физических единиц
- •Учебные материалы по разделам курса физики
- •Физические основы классической механики
- •Примеры решения задач
- •Решение
- •Решение
- •Контрольная работа 1 теоретические вопросы
- •II. Молекулярная физика и термодинамика Основы молекулярно-кинетической теории идеальных газов и термодинамики
- •Механика жидкостей и газов
- •Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Контрольная работа 2 теоретические вопросы
- •III. Электричество и магнетизм Электростатика и постоянный электрический ток
- •Электромагнетизм
- •Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Р ешение
- •Решение
- •Решение
- •Решение
- •Решение
- •Контрольная работа 3 теоретические вопросы
- •IV. Оптика
- •Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Контрольная работа 4 теоретические вопросы
- •V. Физика твердого тела Элементы кристаллографии
- •Свойства твердых тел
- •Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Контрольная работа №5 теоретические вопросы
- •VI. Элементы атомной и ядерной физики Постулаты Бора
- •Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Контрольная работа №6 теоретические вопросы
- •Основные физические постоянные
- •Некоторые астрономические величины
- •Плотности некоторых твердых тел
- •Плотности некоторых жидкостей
- •Плотности некоторых газов
- •Тепловые свойства веществ Твердые тела
- •Упругие свойства некоторых твердых тел
- •Список рекомендуемой литературы
- •Список использованной литературы при составлении задач
- •Варианты контрольных работ
Примеры решения задач
Пример 1. Уравнение движения материальной точки задано уравнением х= А + Bt + Ct3, где А = 2 м, В = 1 м/с, C = –0,5 м/с3. Найти координату х, скорость x и ускорение аx точки в момент времени t = 2 с.
Решение
x = А + Bt + Сt3 A = 2 м B = 1 м/с C = – 0.5 м/с3 t = 2 c |
Координату х найдем, подставив в уравнение движения числовые значения коэффициентов А, В, и С и времени t: x = (2 + 1·2 – 0.5·23) м = 0. Мгновенная скорость по отношению к оси х – это первая производная от координаты по времени
|
x – ? x – ? ax – ? |
Ускорение
точки найдем, взяв первую производную
от скорости по времени ![]() .
.
В момент времени t = 2c: x = (1 – 3·0.5·22) м/с = –5 м/с;
ax = 6·(–0.5)2 м/с2 = –6 м/с2.
Пример 2. Тело вращается вокруг неподвижной оси по закону = A + Вt + Сt2, где A = 10 рад, В = 20 рад/c, C = –2 рад/с2. Найти полное ускорение точки, которая находится на расстоянии r = 0.1 м от оси вращения, для момента времени t = 4 с.
Решение
= А + Bt + Сt2 А = 10 рад B = 20 рад/с С = –2 рад/с2 r = 0.1 м t = 4 с |
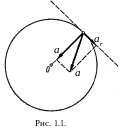
Полное ускорение точки a, которая движется по окружности, находится как геометрическая сумма тангенциального ускорения a, направленного по касательной к траектории и нормального ускорения an, направленного к центру кривизны траектории (рис. 1.1):
Т.к.
векторы a
и an
взаимно перпендикулярны, то модуль
ускорения
|
a – ? |
Модули
тангенциального и нормального ускорения
точки вращающегося тела выражаются
формулами ![]() ,
an
= 2r,
,
an
= 2r,
где – модуль угловой скорости тела, – модуль его углового ускорения.
Подставляя выражения a и an в формулу (1), найдем
![]() .
(2)
.
(2)
Угловую скорость найдем, взяв первую производную угла поворота по времени:
![]() =
B
+ 2Ct.
=
B
+ 2Ct.
В момент времени t = 4 с модуль угловой скорости
= 20 + 2(–2)4] рад/с = 4 рад/с.
Угловое ускорение найдем, взяв первую производную от угловой скорости по времени:
![]() = 2С
=
–4 рад/с2.
= 2С
=
–4 рад/с2.
Подставляя значения , и r в формулу (2), получим
![]() .
.
Пример 3. Ледяная гора составляет угол 30 с горизонтом. По ней пускают снизу вверх небольшой предмет, который за 2 секунды проходит расстояние 16 м, после чего соскальзывает вниз. Найти коэффициент трения между предметом и поверхностью и время соскальзывания.
Решение
|
Это одна из задач на движение тел вдоль наклонной плоскости. В ней требуется и кинематический, и динамический анализ условия. Рассмотрим один из вариантов решения. При движении вверх скорость уменьшается до нуля в верхней точке, предмет движется равнозамедленно прямолинейно. |
|
При движении вниз начальная скорость равна нулю, предмет движется равноускоренно. Путь, пройденный предметом, в обоих случаях одинаков и выражается следующим образом:
![]() ,
,
![]() ,
,
где
![]() и
и
![]() – ускорение и время при движении вверх,
– ускорение и время при движении вверх,
![]() и
и
![]() – то же при соскальзывании.
– то же при соскальзывании.
Приравняв
правые части уравнений, получим
![]() ,
то есть ускорения и квадраты времени
движения связаны обратно пропорциональной
зависимостью. Выразим отношение
ускорений:
,
то есть ускорения и квадраты времени
движения связаны обратно пропорциональной
зависимостью. Выразим отношение
ускорений:
 (1)
(1)
из этого соотношения можно выразить искомое время через отношение ускорений, для этого нужно провести динамический анализ движения.
Следует учесть и показать на рисунках все силы, действующие на предмет при движении вверх (рис. 1.2) и вниз (рис. 1.3) в некоторой промежуточной точке. Векторы всех сил будем считать приложенными в одной точке – центре тяжести предмета.
|
|
Рис. 1.2. |
Рис. 1.3. |
В
обоих случаях предмет взаимодействует
с Землей и плоскостью, при этом на него
действуют: сила тяжести
![]() ,
направленная вертикально вниз, сила
реакции опоры
,
направленная вертикально вниз, сила
реакции опоры
![]() ,
направленная перпендикулярно плоскости,
и сила трения скольжения
,
направленная перпендикулярно плоскости,
и сила трения скольжения
![]() ,
направленная противоположно направлению
движения. Длина отрезка, изображающего
каждую силу, на рис. 1.2 и 1.3 должна быть
одинакова. Равнодействующая сил в обоих
случаях направлена вдоль наклонной
плоскости вниз; согласно закону Ньютона
так же направлено ускорение:
,
направленная противоположно направлению
движения. Длина отрезка, изображающего
каждую силу, на рис. 1.2 и 1.3 должна быть
одинакова. Равнодействующая сил в обоих
случаях направлена вдоль наклонной
плоскости вниз; согласно закону Ньютона
так же направлено ускорение:
![]() .
.
Свяжем систему отсчета для обоих случаев движения с неподвижной точкой, ось Ox направим вдоль ускорения, ось Oy – перпендикулярно к ней. Система отсчета приведена на рис. 1.2.
Запишем II закон Ньютона в векторной форме для движения вверх:
![]() ,
,
Спроектируем все члены уравнения на оси:
![]() (2)
(2)
![]() .
(3)
.
(3)
При
небольших скоростях сила трения
скольжения
![]() прямо
пропорциональна силе, прижимающей
движущийся предмет к поверхности
прямо
пропорциональна силе, прижимающей
движущийся предмет к поверхности
![]() :
:
![]() ,
(4)
,
(4)
где – коэффициент трения.
Выразив
![]() из (3) и подставив
из (3) и подставив
![]() в уравнение (2), получаем:
в уравнение (2), получаем:
![]() .
(5)
.
(5)
Запишем далее II закон Ньютона в векторной форме для движения вниз:
![]() ,
,
в проекциях на оси:
ось
![]() :
:
![]() ,
(6)
,
(6)
ось
![]() :
:
![]() . (7)
. (7)
После преобразований, аналогичных предыдущим, получим:
![]() . (8)
. (8)
Выразив из уравнения (5) и из уравнения (8), имеем:
 .
(9)
.
(9)
Приравняем правые части уравнений (1) и (9):
![]() ,
,
откуда
искомое время
 .
.
Неизвестный
здесь коэффициент трения выразим из
уравнения (5) с учетом того, что
 .
Получим:
.
Получим:

![]()
 .
.
Здесь все известно. Наименования единиц всех членов правой части выражения одинаковы, в результате получается безразмерное число.
Производим вычисления:
 .
.
Получено число, удовлетворяющее условию задачи, оно меньше единицы, как и должно быть.
 .
.
Время соскальзывания больше времени движения вверх, что следует из соответствующего соотношения ускорений.
Пример 4. Шар массой m1, который движется горизонтально с некоторой скоростью , столкнулся с неподвижным шаром массой m2. Удар абсолютно упругий, прямой, центральный. Какую часть своей кинетической энергии первый шар передал второму?
Решение
m1 m2
|
Часть энергии, переданная первым шаром второму выражается соотношением
где Wk1 – кинетическая энергия первого шара до удара; u2 и Wk1 – скорость и кинетическая энергия второго шара после удара. |
Ε – ? |
Как видно из формулы (1), для определения необходимо найти u2. Согласно условию задачи импульс системы двух шаров относительно горизонтального направления не изменяется и механическая энергия шаров в другие виды не переходит. Следовательно
![]() , (2)
, (2)
![]() .
(3)
.
(3)
Решив совместно уравнения (2) и (3) имеем
![]() .
.
Подставив выражение для u2 в формулу (1), получим
 .
.
Из соотношения видно, что часть переданной энергии зависит только от массы столкнувшихся шаров.
Пример 5. Через блок в виде цельного диска, масса которого m = 80 г, перекинута тонкая гибкая нить, к концам которой подвешены грузы массами m1 = 100 г и m2 = 200 г. Определить ускорение, с которым будут двигаться грузы. Трением и массой нити пренебречь.



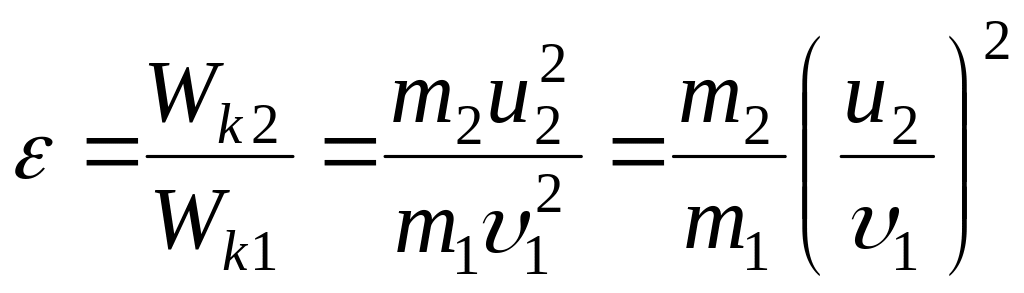 ,
(1)
,
(1)