Властивості логічних операцій кон'юнкції, диз'юнкції та інверсії

Кон'юнкція змінних x₁ і х₂ дорівнює лог. 1 у тому випадку, коли і х₁, і х₂ рівні лог. 1 (звідси виникла назва операції логічне І). Диз'юнкція змінних х₁ і х₂ дорівнює лог. 1, якщо або х₁, або х₂ дорівнює лог. 1 (звідси назва операції логічне АБО). У тих випадках, коли кількість змінних більше двох, їхня кон'юнкція дорівнює лог. 1 при рівності лог. 1 всіх змінних; диз'юнкція рівна лог. 1, якщо хоча б одна зі змінних має значення лог. 1.

У таблиці 15 наведено таблиці істинності для логічних операцій кон'юнкції і диз'юнкції.

Таблиця 15

Аргументи		Логічні операції
х1	х2		х1 • х2	х1 х2
0 0 1 1	0 1 0 1		0 0 0 1	0 1 1 1

У математиці встановлено певний порядок виконання операцій у складному виразі. Наприклад, у виразі х₁ + х₂ • х₃ спочатку виконується операція множення х₂•х₃, а потім операція додавання. Якщо потрібно змінити цей порядок, ви­користовуються дужки. Наприклад, (х₁ + х₂)х₃. Тут спочатку виконується операція в дужках. Подібно до цього для складного логічного виразу те ж встановлено певний порядок виконання операцій: спочатку виконуються операції інверсії, потім операції кон'юнкції й останню чергу операції диз'юнкції. Наприклад, запис логічного виразу х₁ v х₂ • 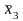v 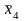• х₂ припускає, що при обчисленні виразу спочатку виконуються операції інверсії і , потім операції кон'юнкції х₂ • й • х₂ і в останню чергу — операції диз'юнкції. Якщо потрібно змінити це правило, використовуються дужки. Наприклад, (х₁ v x₂) • ( v х₄). В цьому випадку спочатку виконуються операції в дужках (а якщо одні дужки вкладені в інші, то спочатку виконуються операції в самих внутрішніх дужках).

Операції кон'юнкції і диз'юнкції мають ряд властивостей:

1 • х = х, 1 v х =1, х • х = х, x v x = х,

, , 0 • х = 0, 0 v x = x, (1)

1 • = 0, = x.

Сполучний закон Переставний закон

х₁ • (х₂ • х₃) = (х₁ • х₂) • х₃, х₁ • х₂ ⁼ х₂ • х₁,

х₁ v (x₂ v х₃) = (х₁ v х₂) v х₃; х₁ v х₂ = х₂ v х₁;

Розподільчий закон (2)

х₁ • (х₂ v х₃) = х₁ • х₂ v х₁ • х₃,

х₁ v (х₂ • х₃) = (х₁ v х₂) • (х₁ v х₃).

Вирази (2) це тотожності, тобто рівності, справедливі при будь-якій комбінації значень змінних. Це може бути підтверджено підстановкою в праву й ліву частини рівностей всіх можливих комбінацій значень змінних із наступним обчисленням логічних значень, до яких приводять вирази в обох частинах рівностей, і їх порівнянням. Така перевірка другого виразу розподільчого закону показана в таблиці 16.

Таблиця 16

Аргументи			Результати обчислення лівої частини рівності		Результати обчислення правої частини рівності
х1	х2	х3	х2 • х3	х1 v х2• х3	х1vх2	х1vх3	(х1vх2)• •(х1vх3)
0 0 0 0 1 1 1 1	0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1	0 0 0 1 0 0 0 1	0 0 0 1 1 1 1 1	0 0 1 1 1 1 1 1	0 1 0 1 1 1 1 1	0 0 0 1 1 1 1 1

Покажемо справедливість так званих формул де Моргана:

,

У виразі , ліва частина стає лог. 1 тільки в тому випадку, якщо х₁ v х₂ = 0, для чого необхідно, щоб х₁ = 0 і_х₂ = 0. Права частина виразу приймає значення лог. 1 тільки при = 1 і = 1, тобто при х₁ = 0 і х₂ = 0. Таким чином, тільки набір х₁ = 0 і х₂ = 0 перетворює в лог. 1 і ліву, і праву частини виразу; при інших наборах значень змінних ліва й права частини виразу будуть мати значення лог. 0, що й доводить справедливість розглянутої рівності.

У виразі і права, і ліва частини стають лог. 0 при х₁ = 1 і х₂ = 1, при інших наборах значень змінних обидві частини рівні лог. 1, що й доводить справедливість даної рівності.

Можна сформулювати наступне правило застосування формул де Моргана до складних логічних виражень. Інверсія будь-якого складного виразу, в якому аргументи (або їхні інверсії) зв'язані операціями кон'юнкції й диз'юнкції, може бути представлена тим же виразом без інверсії зі зміною всіх знаків кон'юнкції на знаки диз'юнкції, знаків диз'юнкції на знаки кон'юнкції й інверсією всіх аргументів. Наприклад, .