1) Усилительное звено (пропорциональное, безынерционное, статическое).

Это звено мгновенно и без искажений воспроизводит входную величину

на выходе (примеры: усилители, редукторы, рычажные передачи).

Уравнение динамики: y(t) = k^.x(t) , где k – коэффициент усиления.

ПФ получается в результате преобразования по Лапласу уравнения движения: y(s) = k^.x(s), откуда

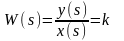
h(t) = k^.[1(t)] w(t) = k^.[δ(t)]

Временные характеристики усилительного звена

2) Апериодическое звено I-го порядка (инерционное)

Примеры: тепловые объекты, любая электрическая цепь, включающая сопротивление и емкость.

Уравнение динамики: , где k > 0 , T > 0

Постоянная времени T характеризует инерционность звена и зависит от величин массы, сопротивления или емкости. Чем больше масса, сопротивление и емкость, тем больше инерционность звена и больше T.

ПФ звена:

Временные характеристики инерционного звена

Обычно считают, что выходная величина достигает своего установившегося значения x_уст не сразу, а постепенно, через время, равное (3-5) T c. В этом проявляется инерционность звена.

Кривая разгона обладает таким свойством: в точке t = T переменная y(t) = 0.63 от x_уст .

3) Апериодическое звено II-го порядка

Звено можно структурно представить в виде последовательного соединения 2-х апериодических звеньев I-го порядка с постоянными времени T₁ и T₂ , поэтому оно не относится к числу элементарных.

Уравнение динамики:

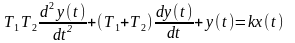
ПФ звена: ,

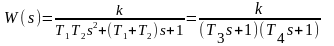где или

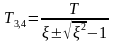
T₁ = T₃ + T₄ ; T₂² = T₃^. T₄ (T₁ > 2T₂ ; T₃ > T₄)

Временные характеристики апериодического звена II-го порядка

По графику переходной характеристики можно определить параметры этого звена. Коэффициент k определяют по установившемуся значению h(∞). Сумма T₃ и T₄ определяется как величина проекции касательной в точке перегиба на линию установившегося значения. Значение T₄ определяется как величина проекции этой же касательной на ось времени.

4) Колебательное звено

Примеры: мембранные исполнительные механизмы, электрические фильтры, поплавковые уравнемеры.

Уравнение динамики:

ПФ звена:

Характеристическое уравнение будет иметь пару комплексно сопряженных корней, если T_Д/T_К < 2 (или T_Д < 2T_К).

Если же T_Д/T_К > 2 (или T_Д > 2T_К), то корни ХУ действительные и звено будет апериодическим II-го порядка.

Соотношение T_К и T_Д очень важно, т.к. T_Д характеризует собой демпфирование собственных колебаний звена, а T_К – их раскачивание.

Величина ξ = T_Д/2T_К , определяющая характер течения переходного процесса, называется коэффициентом затухания (или коэффициентом демпфирования):

- если 0 < ξ < 1, то колебательный процесс затухающий;

- если ξ = 0, то колебательный процесс незатухающий с постоянной амплитудой;

- если ξ < 0, то колебательный процесс становится расходящимся, а звено называют неустойчивым колебательным.

Временные характеристики колебательного звена

5) Консервативное звено

Звено является частным случаем колебательного звена, когда ХУ имеет чисто мнимые корни.

Уравнение динамики:

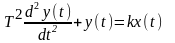
ПФ звена:

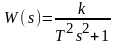
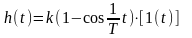
Временные характеристики консервативного звена

6) Интегрирующее звено (нейтральное, астатическое)

Скорость изменения его выходной величины пропорциональна входной величине (примеры: уровень в емкости, счетчики, суммирующие расход вещества или энергии за определенный промежуток времени).

Уравнение динамики: или

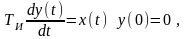
где T_и – постоянная времени интегрирования.

ПФ идеального И-звена получается в результате преобразования по Лапласу: T_иsy(s) = x(s) →

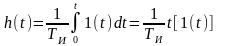
tga = k^.x(t)

Временные характеристики идеального интегрирующего звена

7) Реальное интегрирующее звено

Уравнение динамики:

ПФ звена:

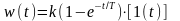
Временные характеристики реального интегрирующего звена

8) Изодромное звено

ПФ звена: где

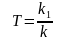
Временные характеристики изодромного звена

9) Дифференцирующее звено

В природе идеального Д-звена не существует. Практически невозможно сделать Д-устройство, дающее производную без искажений, поэтому звено называется идеальным.

Изменение выходной сигнала пропорционально скорости изменения входного сигнала.

Уравнение динамики:

ПФ идеального Д-звена получается в результате преобразования по Лапласу: y(s) = ksx(s) → W(s) = ks

При однократном скачкообразном изменении входной величины скорость изменения в момент скачка равна ∞, а до и после скачка она равна 0. Следовательно, теоретически переходный процесс в таком звене происходит мгновенно. В момент скачка входной величины амплитуда выходной величины теоретически равна ∞.