Определение линейной стационарной системы. Принцип суперпозиции

В теории управления к линейным системам обычно относят те системы, в которых протекающие процессы являются стационарными и описываются линейными ДУ с постоянными или функционально зависящими от времени коэффициентами.

Важным свойством таких систем является их соответствие принципу суперпозиции. В связи с этим определение линейной системы, как правило, дается в следующем варианте: линейными называются системы, подчиняющиеся принципу суперпозиции, который заключается

в том, что реакция объекта на сумму входных сигналов ∑x_i(t) равна сумме реакций на каждый сигнал в отдельности для любых x_i(t).

Математическая запись принципа суперпозиции состоит из двух соотношений:

y(∑x_i(t)) = ∑y_i(t), y(cx(t)) = cy(x(t))

Важно отметить: линейность статических характеристик является необходимым, но не достаточным условием линейности, т.к. выполнение принципа суперпозиции необходимо не только в статике, но и в динамике.

Т.к. большинство объектов управления являются нелинейными, то при определенных условиях нелинейные характеристики могут быть приближенно заменены линейными характеристиками, т.е. производится линеаризация нелинейных зависимостей. Можно также ограничить диапазон работы элемента САУ линейной частью статической характеристики.

Линеаризация нелинейной статической характеристики

Одним из наиболее распространенных способов линеаризации является разложение нелинейной функции в ряд Тейлора в окрестности заданной точки и исключение нелинейных членов разложения.

Пусть статическая характеристика описывается нелинейной n раз дифференцируемой (где n – любое натуральное число) функцией y = f(x), которую необходимо линеаризовать в окрестности точки (x₀ , y₀).

Если в пределах максимально возможных отклонений y и x от x₀ и y₀ функция f(x) мало отличается от линейной функции, то можно f(x) заменить ее приближением

Функция f(x) находится из ряда Тейлора:

Переходя к новой системе координат, 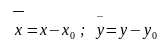, получим линеаризованное уравнение объекта:

Динамическое поведение линейных систем

Система называется динамической, если она описывается дифференциальными, интегральными либо конечными уравнениями, зависящими от времени и называется статической, если в ее описании отсутствует параметр времени.

Наибольший интерес представляет изучение динамического поведения линейной системы, представленной в виде

x(t) y(t)

Основной задачей изучения динамического поведения линейной системы является получение возможности рассчитывать выходной сигнал y(t) для любого известного входного сигнала x(t). В связи с этим необходимо располагать математическим аппаратом для исследования линейной системы.

Основными динамическими характеристиками, используемыми в ТАУ, являются: передаточная функция, дифференциальное уравнение, временные характеристики (амплитудно-фазовая характеристика (АФХ), расширенная АФХ (РАФХ), логарифмические АФХ (ЛАФХ)). Составляющими основных частотных характеристик являются: амплитудно-частотная и фазо-частотная характеристики (АЧХ и ФЧХ), вещественно-частотная и мнимая частотная характеристики (ВЧХ и МЧХ) и соответственно расширенные – РАЧХ, РФЧХ и логарифмические – ЛАЧХ, ЛФЧХ.

Между этими характеристиками существует связь.

Ряд динамических характеристик можно получить экспериментальным путем, а некоторые являются теоретическими. На практике экспериментально получают временные характеристики и частотные (АЧХ и ФЧХ), и уже на основе их записываются ДУ, ПФ, а также расширенные и логарифмические ЧХ. Все это нужно для оценки динамического поведения линейной системы.