Тема 1.6. Метрические задачи
Горизонтальный след прямой
Фронтальный след прямой
n’
a’
b’
m’
x n
a
b
m
Деление отрезка в данном отношении
b’
c’
a’
x 0
a
b c
Отрезок прямой АС разделен точкой В в отношении 5 : 5.
Определить действительную величину отрезка прямой общего положения способом прямоугольного треугольника
B
A
Bb – Aa b’
C a’
c’
H
b
A
b
a
B0
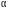
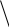
Определение действительной величины треугольника
Определение действительной величины прямоугольника
Определение действительной величины отрезка прямой
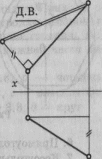
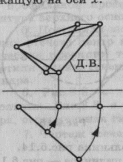
Пересечение пирамиды плоскостью
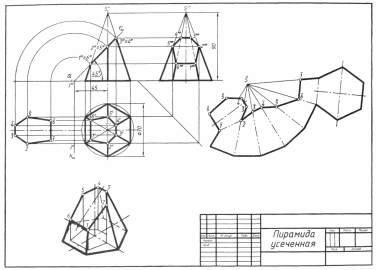
Определить действительную вели чину плоской фигуры способом вращения
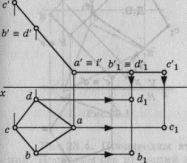
Определить действительную величину плоской фигуры способом перемены плоскостей проекций
b1 a1
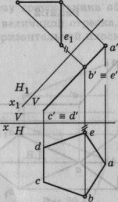
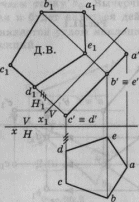
Тема 1.7. Пересечение фигур
Пересечение пирамиды прямой
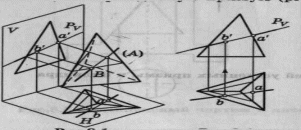
Пересечение призмы плоскостью
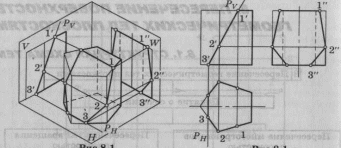
П
ересечение
пирамиды плоскостью
Замкнутая кривая линия (пересекается только боковая поверхность)
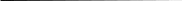
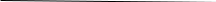
Две части кривой и два отрезка
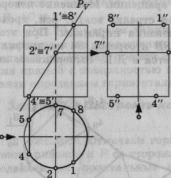
Б
оковая
поверхность конуса
п
ересекается
по образующей
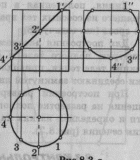
Пересечение цилиндра плоскостью
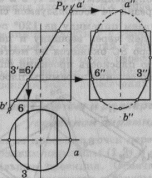
Пересечение конуса плоскостью
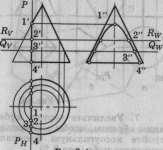
К
акие
фигуры получаются в сечении геометрических
тел
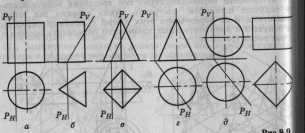
Пересечение геометрических тел
Линия пересечения поверхностей двух многогранников
(пирамиды и призмы)
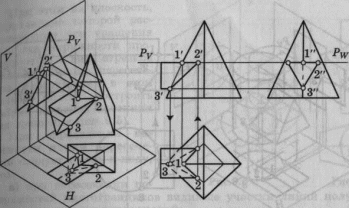
Линия пересечения представляет собой замкнутую ломаную пространственную или плоскую линию. Для построения линии пересечения нужно найти точки пересечения ребер каждого многогранника с гранями другого (или ребер одного с ребрами другого) и найденные точки соединить в определенной последовательности отрезками прямых.
Для определения точек пересечения ребер призмы с гранью пирамиды через ребра проведена горизонтальная вспомогательная секущая плоскость PV, построена линия пересечения пирамиды и на линии пересечения ее с ребрами найдены искомые точки.
Пересечение призмы и пирамиды
e’1 d’1 k’1
2
b
В данном случае горизонтальная проекция линии пересечения поверхностей многогранников совпадает с горизонтальной проекцией призмы и найденные точки следует соединять только на фронтальной проекции. Для определения последовательности соединения фронтальных проекций точек, полученных в пересечении двух многогранников, используют метод Д.Г. Ананова. Он основан на построении схематических развёрток поверхностей пересекающихся тел. Рёбра призмы на схеме расположены вертикально, рёбра пирамиды – наклонно. На развёртки наносим точки, принадлежащие линии пересечения. Отметим на схеме знаком «+» те грани, которые на фронтальной плоскости будут видимы, а знаком «-» те грани, которые на этой плоскости будут невидимы. (Линии на гранях, где сочетаются два «минуса», будут невидимы).
С
D
оставляем схему соединения точек и видимости линий
D’
Соединим точки, лежащие на одной грани: точки 1 и 3, 3 и 5, 5 и 1 – лежат на грани EDE1D1, точки 2 и 7, 7 и 4 – лежат на грани ABS, точки 4 и 8, 8 и 6 – лежат на грани CBS точки 6 и 2 – лежат на грани ACS.
Определим видимость, используя правило: отрезки, принадлежащие двум видимым граням – видимы, отрезки, принадлежащие двум невидимым граням – невидимы, отрезки, принадлежащие двум разным по видимости граням – невидимы.
Отрезки 1-3, 3-5, 7-4, 4-8 – видимы, отрезки 5-1, 2-7, 8-6, 6-2 – невидимы.
На фронтальной проекции соединим отрезки согласно схеме, видимые отрезки – сплошными основными линиями, невидимые – штриховыми линиями.
2
Пересечение многогранника и тела вращения
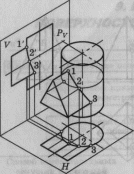
PW
Пересечение тел вращения
3
2
С
оосные
поверхности вращения пересекаются
между собой по окружностям
Е
сли
оси вращения поверхностей пересекаются
и расположены параллельно одной из
плоскостей проекций, то для построения
линии взаимного пересечения используется
способ вспомогательных
секущих сфер
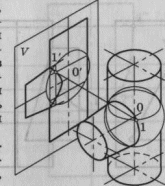
Пересечение конуса и цилиндра
c’
1’
61’
6’
51’
5’
41’
4’
21’
2’
3’
a’
b’
4
3
5
6
c
1
2
a
b
51
61
41
31
