Структурні складові чр:

- тренд ( ft );

- сезонна компонента ( st );

- циклічна компонента ( ct );

- випадкова компонента ( ξt )

а — тренд, що зростає; б — сезонна компонента; в — випадкова компонента

Тренд – траєкторія, що характеризує основну закономірність (тенденцію) зміни соціально-економічного процесу в часі

Слайд № 8

Моделі ЧР:

- адитивна

yt = ft + st + ct + ξt

- мультиплікативна

yt = ft * st * ct * ξt

Процес обчислення функцій

f_t , s_t , с_t , ε_t

називають фільтрацією компонент часового ряду.

Процедура оцінювання детермінантної частини разом з усіма невипадковими компонентами має назву згладжування часового ряду.

Завдання декомпозиції – розкладання часового ряду на систематичні компоненти та випадкові похідні

Слайд № 9

Часові ряди (ЧР) за видом нестаціонарності:

- TS – ЧР із детермінованим поліноміальним трендом;

- DS – ЧР із сталою середньою та наявністю тренду в дисперсії;

- тренд-сезонні – ЧР із трендом, сезонними коливаннями;

- нелінійні динамічні процеси – ЧР із складною структурою.

Тип TS і DS

(порядок інтеграції) - за тестом Діккі-Фуллера,

регресійною статистикою Дарбіна-Ватсона.

Способи перевірки гіпотез

сталості середнього значення чи дисперсії ЧР:

1. метод перевірки різниць середніх рівнів [1, с.171-173];

2. метод Форстера-Стьюарта [1, с.173-175];

3. дослідження автокореляційної функції ЧР (АКФ).

Слайд № 10

Перевірка стаціонарності ряду та наявності

тренду за методом різниць середніх рівнів

1. Формування часового ряду.

2.1. Вихідний часовий ряд розподіляємо на

дві рівні частини: n1 і n2 (n1+n2=n).

2.2. Розрахуємо середні значення і дисперсії

для цих частин за формулами:

; ;

; .

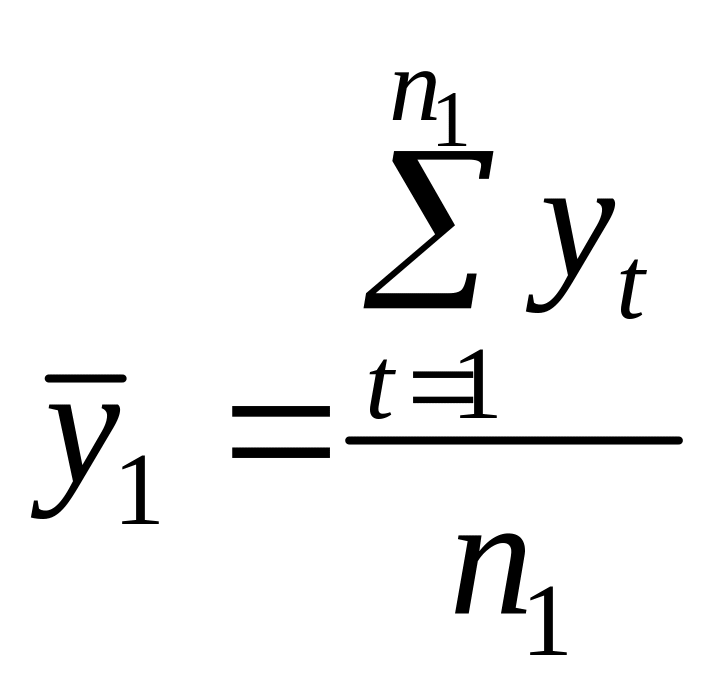2. Перевірка Ч.Р. на стаціонарність за

допомогою F-критерію Фішера

2.1. Розрахуємо F-критерій Фішера.

Якщо Ϭ ²1< Ϭ²2, то F= Ϭ²2/Ϭ ²1;

Якщо Ϭ ²1> Ϭ²2, то F= Ϭ²12/Ϭ ²2.

3. Порівнюємо F i F_tabl.

- +

F > F_tabl.

4. Перевірка Ч.Р. на наявність тренду

за допомогою t-критерію Стьюдента.

4 .1. Розрахункове значення визначаємо за формулою:

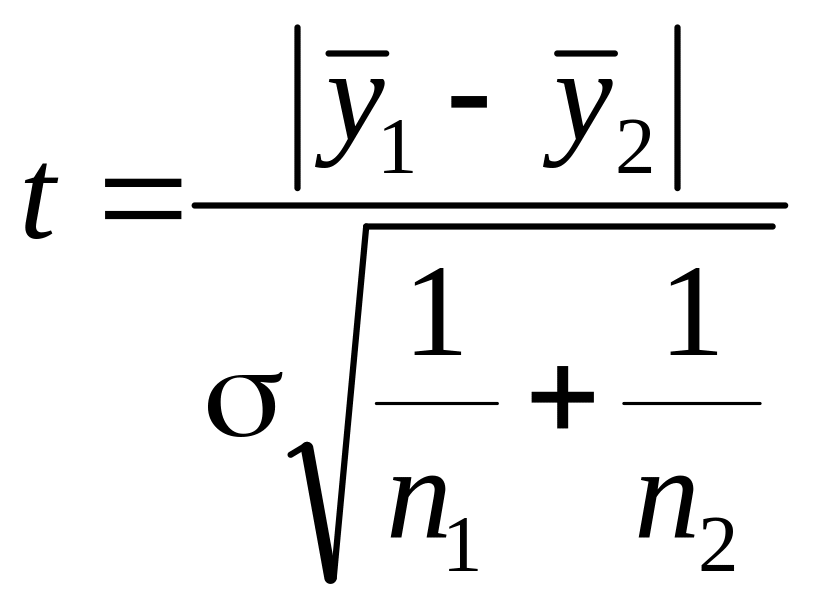, де .

- +

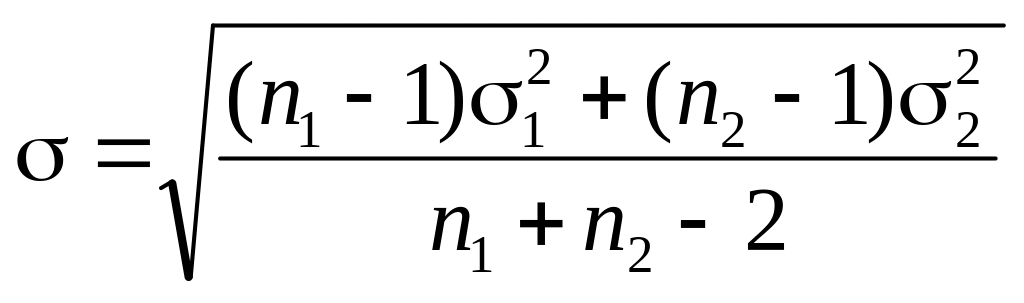t>t_tabl.

Слайд № 11

Метод Форстера-Стьюарта

(алгоритм реалізації)

Крок перший.

Порівняння кожного рівня вхідного ЧР, починаючи з другого рівня, з усіма попередніми - визначення двох числових послідовностей:

t = 2, 3, …, n.

Крок другий.

Розрахунок для ЧР величини зміни рівнів (с) і зміни дисперсії (d):

;

.

Величина c, набуває значення від 0 (усі рівні ряду однакові) до п – 1 (ряд монотонний). Величина d характеризує зміну дисперсії часового ряду та змінюється від [–(п – 1)] — ряд поступово згасає, до (п – 1) — ряд поступово розхитується.

Крок третій

Перевірка гіпотези випадковості:

1) відхилення величини c від математичного сподівання ряду, в якому рівні розташовані випадково, 2) відхи­лення величини d від нуля. Цю перевірку здійснюють на підставі обчислення t-відношення відповідно для середньої та для дисперсії:

; ;

; ,

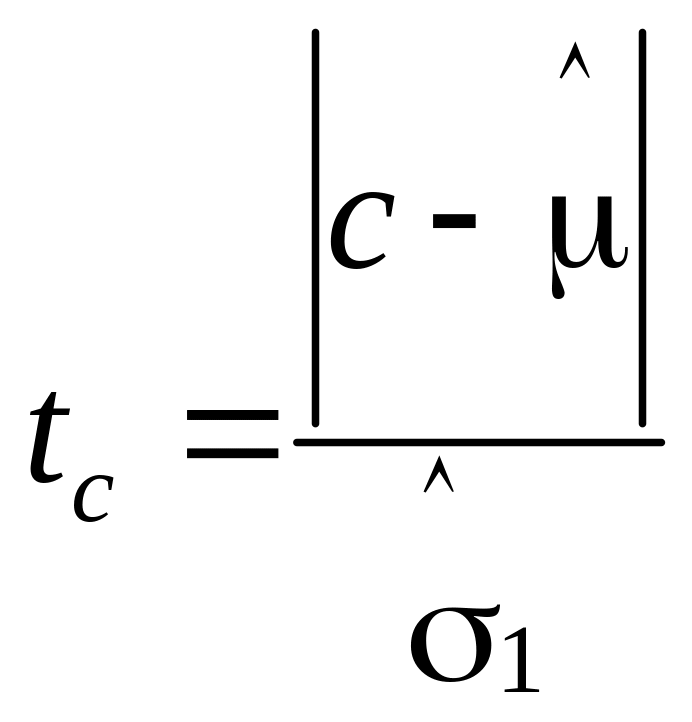Крок четвертий.

Порівняння розрахункових значень t_с i t_d із табличним значенням t-критерію із заданим рівнем значущості t_α. Якщо розрахункове значення t менше за табличне t_α, то гіпотезу про відсутність відповідного тренду приймають, в іншому разі тренд існує.

Слайд № 12