5. Связь между напряженностью поля и потенциалом

Одно и тоже электрическое поле можно охарактеризовать напряженностью и потенциалом. Естественно между этими характеристиками должна существовать связь, и ее легко установить. Как мы знаем, по определению ~ , а , и между ними существует связь:

(12.21)

Разделив (12.21) на величину пробного заряда получим соотношение, связывающее напряженность поля в данной точке пространства и потенциал этой точки:

. (12.22)

Напомним, что в соответствии с определением градиента

. (12.23)

В соответствии с соотношением(12.23) если в пространстве некоторой осью задано направление, то проекция на это направление может быть найдена по формуле:

(12.24)

Часто бывает необходимо решить обратную задачу: по известному распределению в пространстве найти разность потенциалов между двумя точками. В этом случае можно рассуждать так. Работа поля при перемещении заряда из точки 1 в точку 2 определяется соотношением:

(12.25)

С другой стороны эту же работу можно найти по формуле

(12.26)

А значит:

(12.27)

П ри рассмотрении электростатических задач часто используют понятие эквипотенциальной поверхности. Как следует из названия, такой поверхностью называют поверхность, все точки которой имеют одинаковый потенциал. Важным свойством эквипотенциальной поверхности является то, что в каждой точке она перпендикулярна силовым линиям поля (линиям вектора ). Действительно, если бы это было не так (т.е. если бы в данной точке эквипотенциальной поверхности вектор напряженности не был бы ей перпендикулярен и имел бы ненулевую тангенциальную составляющую вдоль некоторого направления), то при перемещении на dl вдоль этого направления потенциал должен был бы получать ненулевое приращение . Это следует из соотношения (12.24) . Но тогда поверхность вдоль этого направления не должна быть эквипотенциальной! Поскольку по условию при перемещении по эквипотенциальной поверхности на dl изменение потенциала , тангенциальная составляющая , и вектор перпендикулярен эквипотенциальной поверхности.

Если потенциальные поверхности проводить так, чтобы разность потенциалов между соседними поверхностями оставалась постоянной, то по густоте эквипотенциальных поверхностей можно судить о величине напряженности электрического поля, как это показано на рисунке 12.3 для точечного положительного заряда.

6. Поле электрического диполя

Э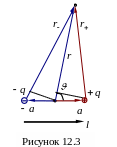 лектрическим диполем называется система двух одинаковых по величине, но противоположных по знаку зарядов, расстояние l между которыми намного меньше расстояния до точек, в которых определяется его поле. Осью диполя называется прямая, проходящая через заряды диполя. На примере поля диполя покажем, как можно использовать вычисление потенциала для нахождения напряженности поля.

Очевидно, что поле диполя обладает осевой симметрией. Это означает, что в любой плоскости, проходящей через ось диполя, картина силовых линий поля одинакова.

Положение точек будем характеризовать радиус-вектором , проведенным из центра диполя или полярными координатами . Пусть положительный заряд имеет радиус-вектор , отрицательный . По определению диполя . Тогда приближенно можно считать, что расстояния от зарядов рассматриваемой точки равны

(12.28)

(12.29)

Тогда потенциал рассматриваемой точки

(12.30)

Учтем, что в силу того, что , можно использовать приближенные соотношения:

; , (12.31)

где .

Тогда

(12.32)

где по определению называют электрическим моментом диполя.

В полярных координатах выражение для потенциала будет иметь вид:

(12.33)

Для того чтобы получить выражение для напряженности поля, найдем проекции и вектора на два взаимно перпендикулярных направления: одно из них определяется движением точки, вызванным изменением при фиксированном , другое  изменением при фиксированном . Проекция

(12.34)

найдем как отношение к приращению расстояния, приходящему при изменении на : это расстояние равно :

(12.35)

Тогда квадрат модуля

. (12.36)

Квадратный корень из (12.36) дает модуль вектора напряженности:

. (12.37)

Рассмотрим структуру поля диполя. Для этого найдем напряженность поля на оси диполя и на прямой, перпендикулярной оси диполя и проходящий через его центр и построим примерный вид силовых линий поля диполя.

Н а оси диполя или , и проекция , поскольку . Проекция составляющей (на направление возрастания r) имеет противоположные знаки с двух сторон от диполя:

, т.е. > 0 для = 0 (справа от диполя) и для (слева от диполя). Следовательно, вектор совпадет по направлению с электрическим моментом диполя и справедливо векторное равенство:

(12.38)

Н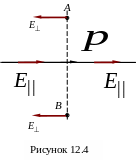 а прямой, перпендикулярной оси диполя и проходящей через его центр . Поэтому , и напряженность определяется :

В точке возрастанию соответствует направление навстречу электрическому моменту диполя, поэтому вектор совпадает по знаку с и направлен противоположно электрическому моменту диполя .

В точке возрастанию соответствует направление вдоль электрического момента диполя, но , и оказывается направленным противоположно электрическому моменту диполя . Поэтому картину силовых линий диполя можно изобразить приблизительно так, как это показано на рисунке 12.5.

Второй важной особенностью поля диполя является тот факт, что модуль вектора напряженности убывает пропорционально . Быстрое убывание модуля вектора напряженности поля является характерной особенностью полей, создаваемых нейтральными в целом системами зарядов. Т ак для системы четырех зарядов квадруполь) напряженность создаваемого поля оказывается пропорциональным , а поле системы восьми зарядов (октуполь) убывает как .

Наконец, необходимо отметить, что взаимодействие электрических моментов молекул является важной составляющей взаимодействия молекул, приводящего к существованию их ван-дер-ваальсовского притяжения на больших расстояниях.