Тема: теплопроводность однослойной цилиндрической стенки при граничных условиях 1 рода

Дана однослойная цилиндрическая стенка внутренним радиусом R₁, наружным радиусом R₂. Известны температуры поверхностей стенки и равны соответственно t_c1 и t_c2. Необходимо определить количество теплоты проходящей через стенку и получить уравнение температурного поля.

При для стационарных условий это уравнение приобретает вид: ;

;

;

;

(1)

c₁ и c₂ определим из ГУ:

Подставим c₁ в 1-е уравнение системы и определим c₂:

Подставим c₁ и c₂ в уравнение (1):

;

Уравнение температурного поля представляет собой логарифмическую зависимость и поэтому температура внутри стенки меняется по логарифмическим кривым.

Плотность теплового потока проходящего через цилиндрическую стенку может быть определена из уравнения Фурье:

Из данного уравнения следует, что плотность теплового потока через изотермическую поверхность радиусом r, зависит от величины этого радиуса, и поэтому плотность теплового потока через внутренние слои стенки будет больше, чем через наружные.

В связи с этим для цилиндрической стенки различают плотности теплового потока через внутренние и наружные поверхности стенки, а также линейную плотность теплового потока, т.е. количество теплоты проходящей через изотермическую поверхность произвольного радиуса r и длиной в 1м.

Определим количество теплоты проходящей через изотермическую поверхность радиуса r:

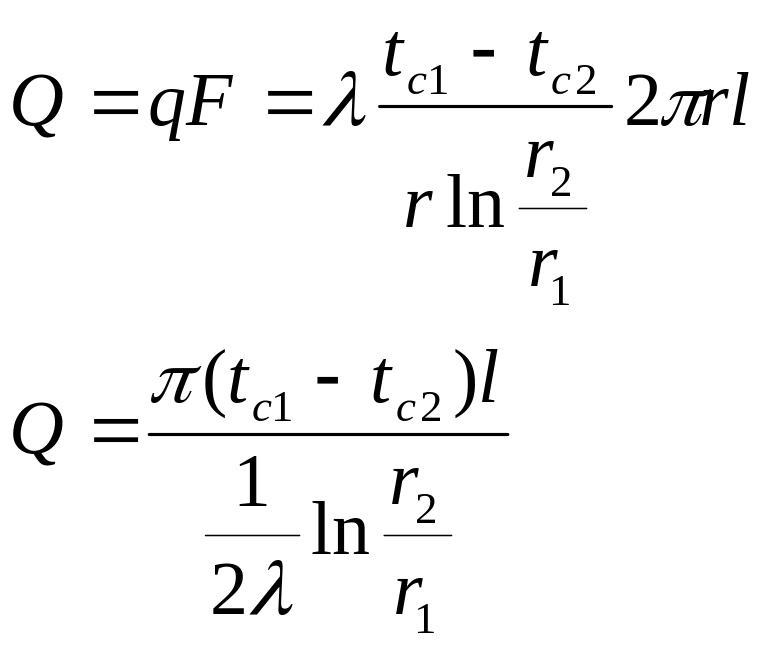
Из этого уравнения следует, что через любую изотермическую поверхность проходит одно и то же количество теплоты.

Линейная плотность теплового потока не зависит от радиуса и поэтому количество теплоты проходящей в 1-цу времени через любую изотермическую поверхность будет одним и тем же.

Тема: конвективный теплообмен

Конвективная теплоотдача, т.е. теплообмен между жидкостью и твердой поверхностью происходит при вынужденном движении жидкости и поэтому связано со скоростью и режимом перемещения подвижной среды. Различают 2 основных режима течения:

1) ламинарный (слоистый);

2) турбулентный (вихревой).

При ламинарном режиме течения параллельные слои жидкости не перемешиваются и направление вектора скорости в каждый момент времени совпадают с направлением движения потока.

При турбулентном режиме направление движения каждой частицы может не совпадать с направлением движения потока.

Режим течения может быть определен по величине безразмерного комплекса называемого числом или критерием Рейнольдса.

, где

W – скорость жидкости (газообразной или капельной);

v – коэффициент кинематической вязкости;

d – геометрический размер канала (диаметр в случае цилиндрического канала или эквивалентный диаметр в случае канала другой формы).

, где

F – площадь поперечного сечения канала;

- периметр.

Критерий Рейнольдса характеризует соотношение между силами инерции и вязкости в потоке.

Коэффициент теплоотдачи, характеризующий интенсивность конвективного теплообмена, зависит от большого числа факторов и поэтому эта величина не может быть определена теоретическим путем, вследствие этого единственным способом определения величины является моделирование процессов, базирующееся на теории подобия.

При этом процесс, протекающий на реальном объекте, моделируется на модели, и полученные результаты переносятся на объект. Для подобия 2-х явлений необходимо:

1) геометрическое подобие;

2) подобие условий однозначности;

3) одноименные критерии для объекта и модели должны быть равны.

В результате моделирования получают уравнения, в состав которых входят безразмерные комплексы, называемые критериями.

Основными критериями являются:

1) Критерий Прандтля

- этот критерий характеризует физические свойства жидкости.

2) Критерий Нуссельта

- характеризует соотношение между интенсивностями конвективного теплообмена и теплопроводности в пограничном слое.

3) Критерий Грасгофа

- характеризует интенсивность свободной конвекции, обусловленная неравномерностью температурного поля в жидкости.

- коэффициент объемного расширения;

g – ускорение свободного падения;

l – геометрические размеры (диаметр в случае цилиндра, длина и высота в случае пластины);

- разность температур жидкости и стенки.

При ламинарном движении жидкости в трубах интенсивность конвективной теплоотдачи зависит от физических свойств жидкости, скорости движения, а также расстояния между рассматриваемым сечением и нагнетателем (насосом).

Нагнетатель в данном случае является источником возмущений (пульсаций) в потоке, интенсивность которых тем выше, чем меньше расстояние.

Для расчета может быть использовано следующее уравнение:

ж, ст – показывают, что данный критерий рассчитывается при средней температуре жидкости или стенки.

d – показывает, что в качестве характерного размера используется диаметр трубы.

- поправочный коэффициент, учитывающий расстояние между сечением и началом трубопровода.

Наличие критерия Грасгофа в данном уравнении указывает на преобладающую роль свободной конвекции при ламинарном движении.

При турбулентном режиме течения жидкости роль свободной конвекции очень мала. Для расчета коэффициента теплоотдачи при турбулентном режиме может быть использовано следующее уравнение:

- поправочный коэффициент, учитывающий расстояние между рассматриваемым сечением и началом трубопровода.

При омывании потоком одиночной трубы характер движения жидкости вблизи поверхности зависит от скорости потока.

При малых критериях Рейнольдса (Re<5) наблюдается гладкое омывание жидкостью как фронтальной, так и тыловой поверхности трубы.

При больших значениях критерия Рейнольдса гладкое омывание наблюдается только в лобовой части тубы, вблизи противоположной поверхности трубы формируется вихревая зона.

В этом случае коэффициент теплоотдачи изменяется вдоль поверхности следующим образом:

Уменьшение при увеличении угла в пределах связано с эффектом прилипания, т.е. увеличением толщины гидродинамического пограничного слоя, т.е. слоя малоподвижной жидкости.

Увеличение при увеличении угла в пределах связано с разрушением гидродинамического слоя вследствие формирования вихревой зоны.

Для расчета коэффициента теплоотдачи могут быть использованы следующие уравнения:

При свободном движении жидкости характер движения зависит от формы размеров и ориентации твердой поверхности.

Для расчета коэффициента теплоотдачи могут быть использованы следующие выражения:

1) горизонтальная труба

2) вертикальная труба (ламинарный режим)

3) вертикальная труба (турбулентный режим)