Контрольні питання

1. За якими ознаками характеризується числова інформація в ЕОМ?

2. Дати визначення системи числення? Навести приклади систем числення.

3. Дати пояснення позиційної системи числення? Навести приклади.

4. Що таке непозиційна система числення? Навести приклади.

5. Дати визначення поняття машинне подання?

6. Перетворення числа в десятковій системі числення в число, представлене в двійковій системі. Навести конкретні приклади.

7. Скільки і яких цифр потрібно, щоб будь-яке число можна було записати у сімковій системі числення? А в дванадцятковій?

8. Дати пояснення особливостям перетворення чисел з десяткової системи числення у вісімкову. Навести конкретні приклади.

9. Дати пояснення особливостям перетворення чисел з десяткової системи числення у шістнадцяткову. Навести конкретні приклади.

10. Поясніть взаємозв'язок між прямим двійковим, оберненим і доповняльним кодами.

11. Поясніть особливості коду Грея та сфери його використання.

12. Назвати особливості представлення від’ємних чисел.

13. Що називають розрядною сіткою?

14. Що називають форматом числа?

15. Навести основні форми представлення чисел.

16. Поясніть суть запису двійкових чисел у формі з фіксованою комою. У чому полягають недоліки такого способу запису?

17. Поясніть особливості запису у формі з плаваючою комою.

18. Яким чином здійснюється запису чисел у розрядну сітку?

19. Що називають операндом?

20. Поясніть послідовність виконання арифметичних операцій додавання і віднімання у двійковій системі числення при різних знаках зменшуваного і від'ємника.

21. Додавання двійкових чисел з фіксованою комою.

22. Віднімання двійкових чисел з фіксованою комою.

23. Поясніть послідовність виконання множення двійкових чисел з фіксованою комою.

24. Дати визначення часткового добутку?

25. Ділення двійкових чисел з фіксованою комою.

26. Додавання двійкових чисел з плаваючою комою.

27. Віднімання двійкових чисел з плаваючою комою.

28. Поясніть послідовність виконання операції множення у двійковому коді.

Вправи і завдання

1. Який вигляд матиме у двійковій системі числення десяткове число 0,127₁₀?

2. Перетворіть у десяткову систему числення числа записані у двійковій: 11₂, 101₂, 10000₂.

3. Перетворіть числа 118, 57, 195, 234, що подані в десятковій системі числення, у двійкову, вісімкову та у шістнадцяткову системи.

4. Знайдіть суму таких пар чисел, заданих у десятковій системі числення: 38 і 42; 22 і 112; 25 і (-234), перевівши їх спершу в двійкову систему числення.

5. Виконайте операцію множення двох чисел: а=1101₂ та b=1011₂.

Виконайте операцію ділення двох чисел: а=1101110₂ та b=1010₂.

Розділ 2. Логічні основи еом

2.1 Алгебра логіки (ал)

З цього розділу ви зможете:

• дізнатися про основні положення алгебри логіки;

• розібратися з основними логічними операціями;

• засвоїти реалізацію логічних операцій на логічних елементах;

• засвоїти принципи мінімізації булевих функцій методом Квайна

• засвоїти принципи мінімізації булевих функцій методом карт Карно.

Алгебра логіки (АЛ) є теоретичною основою комп'ютерної схемотехніки. Це наука, яка використовує математичні методи для розв’язання логічних задач. Алгебру логіки називають булевою на честь англійського математика Дж. Буля. Основним предметом булевої алгебри є висловлювання.

Висловлюванням називається просте твердження, про яке можна стверджувати: істинне воно або хибне. Зазвичай прості висловлювання в АЛ позначаються буквами будь-якого алфавіту: А,ВС,...,X,Y,Z. Істинність або хибність висловів називають значеннями істинності. В АЛ прийнято позначати істинність висловлювання числом 1, а хибність – числом 0. Приклад. Нехай А=1, В=0. Значить, А – істинне, В – хибне.

У даний час головна задача АЛ – аналіз, синтез і структурне моделювання будь-яких дискретних скінчених систем.

Змінну із скінченним числом значень (станів) називають перемикальною, а з двома значеннями – булевою. Функція, яка має як і кожна її змінна скінчене число значень, називається перемикальною (логічною). Логічна функція, число можливих значень якої і кожної її незалежної змінної дорівнює двом, є булевою. Таким чином, булева функція – це є окремий випадок перемикальної.

Операція – це чітко визначена дія над одним або декількома операндами, яка створює новий об’єкт (результат).

Основними булевими операціями є заперечення, кон'юнкція, диз'юнкція, які можна задати за допомогою таблиць істинності.

Запереченням висловлювання А є таке висловлювання, яке істинне, коли А хибне, і хибне, коли А істинне. Воно позначається через і читається «не А». Заперечення розповсюджується на один операнд.

Таблиця 2.1. Логічні значення операції заперечення

А
1	0
0	1

Кон'юнкція двох висловлювань є складне висловлювання. Вона відноситься до групи бінарних операцій. У разі істинності обох висловлювань істинна і сама кон'юнкція, інакше вона помилкова. Вона також помилкова, якщо помилкове будь-яке з двох висловлювань. У загальному випадку число висловлювань може бути і більше двох. Операція кон'юнкції позначається «А^В» і читається «А і В». Кон'юнкцію також називають логічним множенням і позначають знаком &.

Таблиця 2.2. Логічні значення операції кон'юнкції

A	B	A^B
1	1	1
0	1	0
1	0	0
0	0	0

Диз'юнкція двох висловлювань – складний, бінарний, вислів. Вона хибна у разі помилковості обох складових її висловлювань і істинна в решті випадків. Диз'юнкція позначається AVB або А+В і читається «А або В». Інша назва цієї операції – логічне додавання.

Таблиця 2.3. Логічні значення операції диз'юнкції

A	B	AVB
1	1	1
0	1	1
1	0	1
0	0	0

Для булевих операцій заперечення, диз'юнкції і кон'юнкції справедливі такі закони, властивості й тотожності:

• комутативність (переміщувальний закон):

Х₁+X₂=X₂+X₁;

Х₁•X₂=X₂•X₁;

• асоціативність (сполучний закон):

Х₁(Х₂+X₃)=Х₁Х₂+Х₁Х_3;

Х₁+(Х₂X₃)=(Х₁+X₂)(Х₁+X₃);

• закон поглинання:

Х₁+X₁X₂=X₁;

Х₁(Х₁+X₂)=Х₁;

• закон склеювання:

Х₁X₂+X₁=X₁;

(Х₁+X₂)(Х₁+ )=Х₁;

• властивості заперечення і констант:

Х+0=X; Х•0=0;

Х+1=1; Х•1=X; ;

• закон де Моргана:

;

;

Будь-який складний вираз, утворений з простих висловлювань, називається формулою АЛ. Дві формули АЛ, утворені з n простих висловлювань А₁, А₂, А_n, називаються рівносильними в тому випадку, якщо для кожної з цих комбінацій обидві формули АЛ матимуть однакові значення істинності. Оскільки існують в точності різних комбінацій значень істинності n простих висловлювань і для кожної з цих комбінацій складний вираз може бути або істинним, або помилковим, то може бути різних функцій АЛ, які можуть бути побудовані з n даних простих висловлювань. Зокрема, для двох двійкових змінних можна побудувати 16 різних висловлювань АЛ, тобто скласти 16 нерівносильних складних логічних виразів. Ці вирази містять усі описані раніше логічні зв'язки (заперечення виключається, оскільки це функція однієї змінної).

Логічні операції кон'юнкції, диз'юнкції, співвідношення, еквівалентності, заперечення еквівалентності (^,V,--, ,~, ) не є незалежними, і можуть бути виражені одина через одну. Зокрема з них можна виділити системи логічних операцій із їхньою допомогою представити взагалі усі функції АЛ. Це системи: --,^,V, або --,^, або --,V . Крім того, існує операція заперечення кон'юнкції , через яку (одну) може бути виражена будь-яка функція АЛ. Усі перераховані системи вважаються функціонально повними. Зокрема операція , що стверджує несумісність двох висловлювань, позначається A|B і називається функцією Шеффера, при цьому заперечення, кон'юнкція і диз'юнкція виражаються так: , , .

Електронна схема, що реалізує операцію Шеффера, є функціональним універсальним елементом. За її допомогою можуть бути побудовані будь-які функціональні схеми дискретних автоматів.

Довільну булеву функцію можна задавати різними способами: словесним описанням, часовими діаграмами, геометричними фігурами, графами, таблицями істинності та аналітичними виразами.

Словесний опис деякої булевої функції F(X₁, Х₂) можна представити так: F=1 при X₁Х₂=1 і F=0, якщо X₁Х₂=0. Таку функцію можна зобразити часовою діаграмою (рис. 2.2, а) або геометрично за допомогою двовимірного куба, у якому точками виділені одиничні вершини (дана функція набуває значення одиниці на наборі <1, 1>) (рис. 2.2, б), а також графом, де вершини відображають значення нуля і одиниці, а на орієнтованих дугах змінні вказують на умови переходів (рис. 2.2, в).

Рис. 2.2. Способи задавання булевих функцій

До нових булевих функцій (операцій) відносяться такі.

Еквівалентність двох висловлювань – бінарний вислів. Вона істинна тоді, коли значення істинності висловлювань однакові і хибна навпаки. Позначається А~В і читається «А еквівалентно В».

Таблиця 2.4. Логічні значення операції еквівалентністі

A	B	A~B
1	1	1
0	1	0
1	0	0
0	0	1

Сума за модулем два (виключальне АБО, заперечення еквівалентності) двох висловлювань є бінарним висловом, яка хибна у тому випадку, коли А і В мають різні значення.

Таблиця 2.5. Логічні значення операції заперечення еквівалентності

A	B	A B
1	1	0
0	1	1
1	0	1
0	0	0

Імплікація двох висловлювань є бінарним висловом, яка хибна тільки у тому випадку, коли А істинне, а В помилкове. Її позначають через , і читається так «якщо А, то В». Імплікація не припускає обов'язковий зв'язок по сенсу між умовою А і слідством В (хоча і не виключає такий зв'язок).

Таблиця 2.6. Логічні значення операції імплікації

A	B
1	1	1
0	1	1
1	0	0
0	0	1

Булеві функції одного і двох аргументів називають елементарними. Схему, яка здійснює елементарну логічну операцію, називають логічним елементом. Сукупність взаємозалежних елементів з формальними методами описання називається логічною схемою.

Для реалізації однієї і тієї ж логічної функції існує велика кількість різних електронних схем. З метою спрощення документації були введені символи, так звані логічні елементи, які позначають тільки логічну функцію і не розкривають внутрішню будову схеми.

Основні логічні елементи мають, як правило, один вихід (Y) та декілька входів, число яких дорівнює числу аргументів (Х₁, Х₂, Х₃,…, Х_n). На електричних схемах логічні елементи зображуються у вигляді прямокутників з виводами для вхідних (ліворуч) і вихідних (праворуч) змінних. Всередині прямокутника зображується символ, який вказує на функціональне призначення елемента.

Назви і умовні графічні позначення основних логічних функцій, які застосовуються в комп’ютерній схемотехніці наведені нижче:

Операція кон'юнкція реалізується логічним елементом «І»

Операція диз'юнкція реалізується логічним елементом «АБО»

Операція заперечення реалізується логічним елементом «НІ»

О перація заперечення еквівалентністі реалізується логічним елементом «Виключальне АБО»

Операція еквівалентность реалізується логічним елементом

Операція імплікація реалізується логічним елементом

Операція заборона реалізується логічним елементом

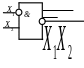
Рядом з однофункціональними елементами (І, АБО, НІ), широко використовуються двофункціональні (АБО-НІ, І-НІ)

АБО-НІ І-НІ

Будь-яку логічну функцію можна реалізувати на логічних елементах. Наприклад

Рис. 2.1. Схема для реалізації логічної функції _.

Приклад. Необхідно скласти схему, на виході якої при В>А, де А і В є однозначними двійковими цифрами, встановлюється логічна одиниця 1. Складаємо табл. 2.7.

Таблиця 2.7

А	В	Y
0	0	0
0	1	1
1	0	0
1	1	0

З таблиці маємо, що Y=1 при виконанні тільки однієї умови, коли А=0 і В=1. Логічна функція записується у вигляді . Вона реалізується на таких логічних елементах:

Рис. 2.3. Схема для реалізації логічної функці _.