- 8 -

Глава 1. Основные понятия

Содержание

1.1 Понятие дифференциального уравнения. Примеры уравнений 2

1.2. Формы представления уравнений 3

1.3. Формы представления решения дифференциального уравнения 4

1.4. Геометрическая интерпретация решения дифференциального уравнения 4

1.5. Задачи, связанные с дифференциальными уравнениями 7

1.1 Понятие дифференциального уравнения. Примеры уравнений

Cоотношения между неизвестной функцией, ее производ­ными и независимыми переменными называются дифференциальными уравне­ниями. Уравнения, содержащие производные лишь по одной из независимых переменных, называют­ся обыкновенными дифференциальными уравнениями. Уравнения, содержащие производные по многим независимым переменным, называются уравнениями в частных производных.

Алгебраические уравнения не описывают в достаточной мере процессы реального мира. Алгебраические уравнения описывают лишь установившуюся, статическую картину. В то же время реальные процессы связаны с инерционностью объектов; скорость протекания процессов часто зависит от многих факторов. Для описания таких процессов нужны дифференциальные уравнения.

Пример 1.1. Уравнение радиоактивного распада. Физический закон, описывающий процесс радиоактивного распада, состоит в том, что скорость распада пропорциональна количеству не распавшегося к данному моменту вещества:

Здесь m – масса вещества, t – текущее время (независимая переменная), – постоянная распада, характеризующая данное вещество. Знак минус означает, что скорость отрицательна – количество вещества уменьшается. Данное уравнение является уравнением с разделяющимися переменными, и оно легко решается. Перепишем уравнение иначе

(1.1)

и проинтегрируем правую и левую часть:

Здесь C – постоянная интегрирования, которую можно определить из условия: – исходная масса вещества в нулевой момент времени равна m₀. Получаем в итоге C = ln m₀ и

– количество не распавшегося вещества уменьшается по экспоненциальному закону.

О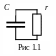 тметим, что в некоторых случаях одно и то же уравнение может описывать процессы разной физической природы. Например, рассмотрим процесс разряда конденсатора в цепи, представленной на рис 1.1. Обозначим через V(t) напряжение на обкладках конденсатора в момент t. Соответственно, заряд конденсатора равен q=VC. Напряжение на сопротивлении равно , где – сила тока в цепи. Сумма напряжений в замкнутой цепи равна нулю:

.

Преобразовав это выражение, придем к уравнению, аналогичному уравнению (1.1):

где = r C называется постоянной времени.

П ример 1.2. Уравнение колебаний. Составим уравнение для колебательного контура, представленного на рис 1.2. Обозначим, как и прежде, V(t) – напряжение на обкладках конденсатора, – сила тока в цепи. Напряжение на катушке индуктивности L равно , и сумма напряжений в замкнутой цепи равна нулю:

.

Обозначив – коэффициент затухания, – частота собственных колебаний, перепишем уравнение в виде:

. (1.2)

Имеем линейное дифференциальное уравнение второго порядка. Решение этого уравнения описывает процесс затухающих колебаний. Если <<₀ (коэффициент затухания мал), V(0)=V₀ и ток в начальный момент равен нулю , то процесс колебаний описывается формулой:

.

Отметим, что аналогичное уравнение описывает колебания маятника (в предположении, что амплитуда колебаний невелика).

Пример 1.3. Движение тела под воздействием внешней силы. В соответствии со вторым законом Ньютона произведение массы тела на ускорение равно воздействующей силе:

. (1.3)

Если рассматривается прямолинейное движение, то r и F – скалярные функции. Если при этом сила – постоянная величина, то дважды проинтегрировав это уравнение и введя обозначения: a=F/m – ускорение тела, r₀, v₀ – положение и скорость тела в начальный момент t=0, – получим закон движения с постоянным ускорением:

.

При рассмотрении движения в трехмерном пространстве имеем систему из трех уравнений, описывающих движение по трем осям координат. Приложенная сила может зависеть от положения и скорости тела, а также от времени, так что уравнение, описывающее закон движения, в общем случае будет более сложным.

Пример 1.4. Уравнения в частных производных:

– уравнение, описывающее распространение тепла в стержне.

– уравнение поперечных колебаний струны.