2. Формуланы, есте сақтауға ыңғайлырақ мына түрде жазуға болады:

(сыртқы тік жақша абсолют шаманың белгісі).

Айталық, жазықтықта М₁М₂ кесіндісі берілсін, М осы кесіндінің кез-келген М₂ - ден басқа нүктесі болсын. М нүктесі М₁М₂ кесіндісін λ қатынасында бөліп тұрсын, яғни:

М₁(х₁;у₁), М₂(х₂;у₂) нүктелері анықтап тұрған кесіндіні λ қатынасында бөлетін М(х;у) нүктесінің координатасын төмендегі формулалар арқылы есептеуге болады:

λ=1 болғанда кесіндінің ортасы болып тұрған нүктенің координатасын табатын формула шығады:

Кей жағдайларда Декарттық координаталар системасынан басқа координаталар системасын қолдану ыңғайлырақ болады. Сондай координаталар системасының бірі – полярлық координаталар системасы.

Полярлық координаталар системасында М нүктесі полюс деп аталатын О нүктеден қашықтығы (|ОМ|=ρ) мен ОМ кесіндінің полярлық ось деп аталатын ОЕ түзуімен жасайтын бұрышы φ арқылы анықталады. ОМ кесіндісін нүктенің полярлық радиус-векторы деп атайды. Егер полярлық осьтен полярлық радиус-векторға қарай бұрылу бағыты сағат тіліне қарсы бағыт болса, онда бұл бұрыш оң таңбалы болады, кері бағытты теріс бағыт деп есептейді.

Нүктенің декарттық координаталары мен полярлық координаталары арасында мынадай байланыс бар (полярлық осьті абсцисса осі деп есептейміз, ал ордината осі полярлық осьпен оң бағытта 90 градус бұрыш жасайды).

Векторлар және оларға қолданылатын амалдар

Вектор, вектордың ұзындығы, нольдік вектор, бірлік вектор, тең векторлар, коллинеар және компланар векторлар, векторларды қосу мен алудың параллелограм ережесі, векторларды санға көбейту ұғымдарымен мектеп курсындағы математикадан таныссыздар. Дегенмен солардың кейбіреулерін естеріңізге сала кетелік.

Суретте векторларды стрелка (бағытталған кесінді) түрінде кескіндейді. Вектор өзінің ұзындығы мен бағыты арқылы толық сипатталады. Жазықтықтағы аналитикалық геометрияда вектор оның координаталары деп аталатын екі сан арқылы беріледі. Векторды оның басы мен соңында жатқан нүктелерді көрсету арқылы да сипаттайды. Бұл жағдайда, оны кәдімгі бағытталмаған кесіндіден ажырату үшін үстіне сызықша немесе стрелка қояды. Мысалы болмаса . Кейде векторды бір ғана әріппен де белгілейді ( ). Егер векторының координаталары a₁, a₂ сандары болса деп жазады.

Кейде, айтылып отырған тақырыптан вектор туралы айтылып отырғаны түсінікті болатын болса, онда әріп үстіндегі сызықша немесе стрелканы жазбай-ақ қоюға да болады. Кей әдебиеттерде векторды жуан әріптермен белгілейді. Біз ыңғайына қарай осы белгілеулердің бәрін де қолданамыз.

Е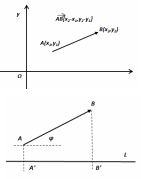 гер M₁(x₁,y₁), M₂(x₂,y₂) нүктелері берілген болса векторының координаттары төмендегідей болып есептеледі:

Бізге L осі мен АВ векторы берілсін. АВ векторының L осіне проекциясы А’В’ кесіндісі болсын. Осы проекцияның ұзындығы АВ векторының ұзындығын осы вектор мен L осінің арасындағы бұрыштың косинусына көбейткенге тең болады:

Кеңістікте вектордың координаталары үш сан болады. векторының бағыттаушы косинустары деп осы вектордың координаталар осьтерімен жасайтын бұрыштарының косинустарын айтады. векторының бағыттаушы косинустары төмендегідей формулалармен есептеледі:

Векторларға қосу, алу амалдарын қолдануға болады. Векторларды санға көбейтуге де болады.

Анықтама 1. a, b векторларының қосындысын табу үшін a векторының соңына жалғастырып b векторын салады, сосын a векторының басынан басталып b векторының соңынан бітетін вектор осы екі вектордың қосындысы деп аталады да a+b деп белгіленеді.

Егер a{a₁,a₂,a₃}, b{b₁,b₂,b₃} болса, онда a+b={a₁+b₁, a₂+b₂, a₃+b₃} болады.

Анықтама 2. a векторына қосқанда қосындысы b болатын векторды b мен a векторының айырмасы деп атаймыз да былай белгілейміз b-a.

Егер a{a₁,a₂,a₃}, b{b₁,b₂,b₃} болса, онда b-a={b₁-a₁, b₂-a₂, b₃-a₃} болады.

Анықтама 3. a векторы мен λ санының көбейтіндісі деп ұзындығы |λ||a| болатын, ал бағыты λ>0 болса a векторының бағытымен бірдей болатын; ал λ<0 болса бағыты a векторына қарама қарсы болатын векторды айтады. Ол вектор λa арқылы белгіленеді.

Егер a{a₁,a₂,a₃} болса, онда λa={λa₁,λa₂,λa₃} болады.

Анықтама 4. Екі нольден ерекше a,b векторларының скалярлық көбейтіндісі деп олардың ұзындықтары мен екеуінің арасындағы бұрыштың косинусының көбейтіндісін айтады да (ab) деп белгілейді, яғни:

(ab)=|a||b|cos(a^b).

Егер a{a₁,a₂,a₃}, b{b₁,b₂,b₃} болса, онда

(ab)=a₁b₁+a₂b₂+a₃b₃

болады.

Скалярлық көбейтіндінің қасиеттері:

1. (ab)=(ba);

2. ((λa)b)=λ(ab);

3. (a(b+c))=(ab)+(ac);

4. (aa)=a²=|a|²;

5. (a^b)=90⁰→(ab)=0;

6. cos(a^b)=(ab)/(|a||b|)

7. Егер векторлардың координаталары пропорционал болатын болса, олардың бағыттары параллель (коллинеар) болады

А нықтама 5. Екі a, b вектордың векторлық көбейтіндісі деп төмендегі шарттарды қанағаттандыратын c векторын айтады:

1. a, b векторларының әрқайсысына перпендикуляр;

2. ұзындығы |a||b|sin(a^b) болады;

3. c векторының соңынан қарағанда a векторынан b векторына қысқа жолмен бұрылу сағат тіліне қарсы бағытта болады.

Векторлық көбейтінді [a,b] болмаса axb деп белгіленеді.

Векторлық көбейтіндінің геометриялық мағынасы. Векторлық көбейтіндінің нәтиежесінде алынатын вектордың ұзындығы көбейткіш векторлар қабырғалары болатын параллелограммның ауданына тең болады.

Векторлық көбейтіндінің қасиеттері:

1. 

2. 

3. 

4. 

Егер a{a₁,a₂,a₃}, b{b₁,b₂,b₃} болса, онда

Векторлардың аралас көбейтіндісі

Анықтама. a, b, c векторлары берілсе, олардың аралас көбейтіндісі деп (axb)c формуласымен анықталатын санды айтады. Аралас көбейтіндіні (abc) түрінде белгілейді.

Аралас көбейтінің абсолют шамасы, қабырғалары сол аралас көбейтіндіні құрап тұрған векторлар болатын параллелепипедтің көлеміне тең болады.

Аралас көбейтіндінің қасиеттері:

1. ;

2. ;

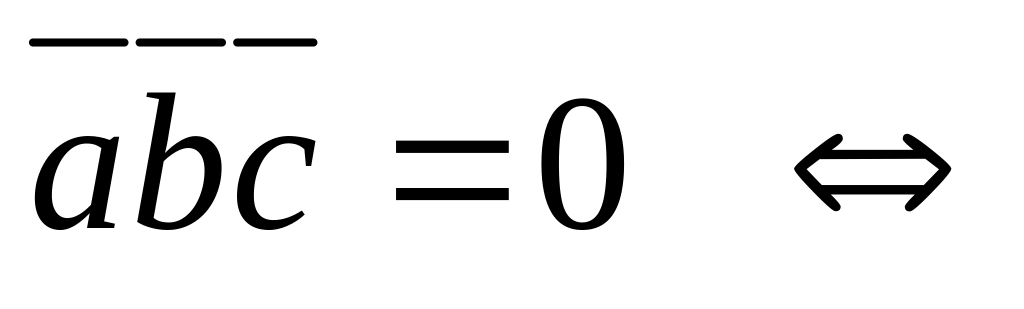3. a, b, c векторлары бір жазықтықтықта жатады (бір жазықтыққа параллель), яғни компланар векторлар болады.

Егер a{a₁,a₂,a₃}, b{b₁,b₂,b₃}, c{c₁,c₂,c₃}, онда

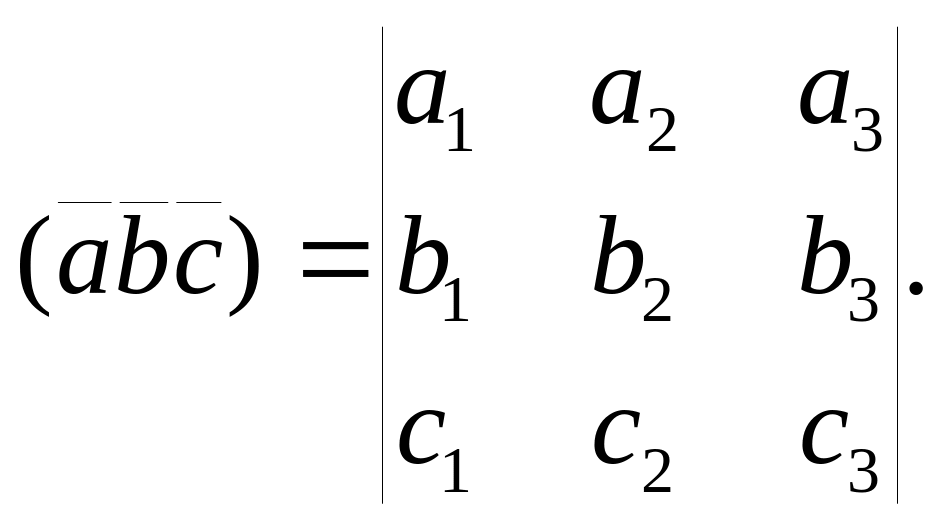
Жазықтықтағы түзу

Анықтама. Егер L сызығының бойында жатқан нүктелердің координаталары, және тек солардың ғана координаталары F(x, y)=0 теңдеуін қанағаттандыратын болса, онда F(x, y)=0 теңдеуін L сызығының теңдеуі деп атаймыз.

Егер теңдеуде х, у белгісіздерінің бірінші дәрежесі ғана қатысып отыратын болса, ондай теңдеуді бірінші дәрежелі теңдеу деп, немесе сызықтық теңдеу деп атайды.

Жазықтықтағы декарттық координаталар системасында түзудің теңдеуі бірінші дәрежелі теңдеу болады:

Ax+By+C=0 (1)

Егер B≠0 болса, онда (1) теңдеуді (теңдеуді B санына бөліп –A/B=k, –C/B=b белгілеулерін енгізеді де, y айнымалысы жоқ мүшелерді теңдеудің оң жағына жинақтап, төмендегідей түрге келтіруге болады:

у=kх+b (2)

(1) теңдеуді түзудің жалпы теңдеуі деп атайды, ал (2) теңдеуді бұрыштық коэффициент арқылы берілген теңдеу деп айтады. (2) теңдеудегі k саны бұрыштық коэффициент деп аталынады, оның шамасы түзудің Ox осінің оң бағытымен жасайтын бұрышының тангенсіне тең болады.

Жазықтықта түзуді әртүрлі әдістермен беруге болады. Төменде түзу әртүрлі әдістермен берілген кезде теңдеуін қалай табуға болатындығы көрсетілген.

1. Түзудің бұрыштық коэффициенті k-ға тең, ал түзу M₁(x₁,y₁) нүктесі арқылы өтсін. Сонда оның теңдеуін былай жазуға болады:

y-y₁=k(x-x₁) (3)

2. Берілген әртүрлі екі M₁(x₁;y₁), M₂(x₂;y₂) нүкте арқылы өтетін түзудің теңдеуі төмендегі формуламен табылады:

3. Түзу Ox, Oy осьтерінен ұзындықтары a, b сандарына тең кесінділерді қиып өтсін. Онда ол түзудің теңдеуін төмендегідей қылып жазуға болады

(5) теңдеуді түзудің кесінділер бойынша теңдеуі деп айтады.

4. Төмендегі теңдеуді түзудің нормаль теңдеуі деп айтады

мұнда р-координаталардың бас нүктесінен қарастырып отырған түзуге түсірілген перпендикулярдың ұзындығы, ϕ - осы перпендикулярдың Ох осінің оң бағытымен жасайтын бұрышы.

5. Берілген a{m,n} бағытына параллель болатын, M₁(x₁,y₁) нүктесі арқылы өтетін түзу теңдеуі былай жазылады: