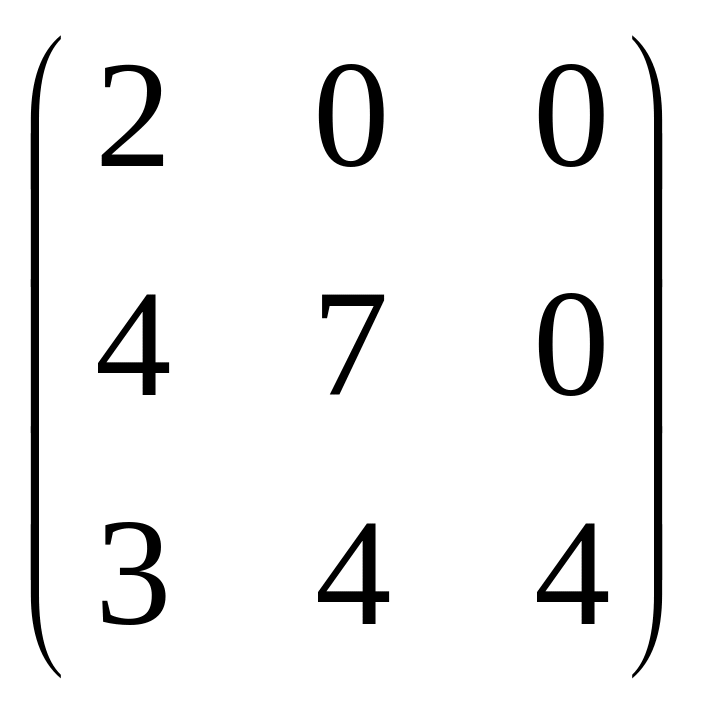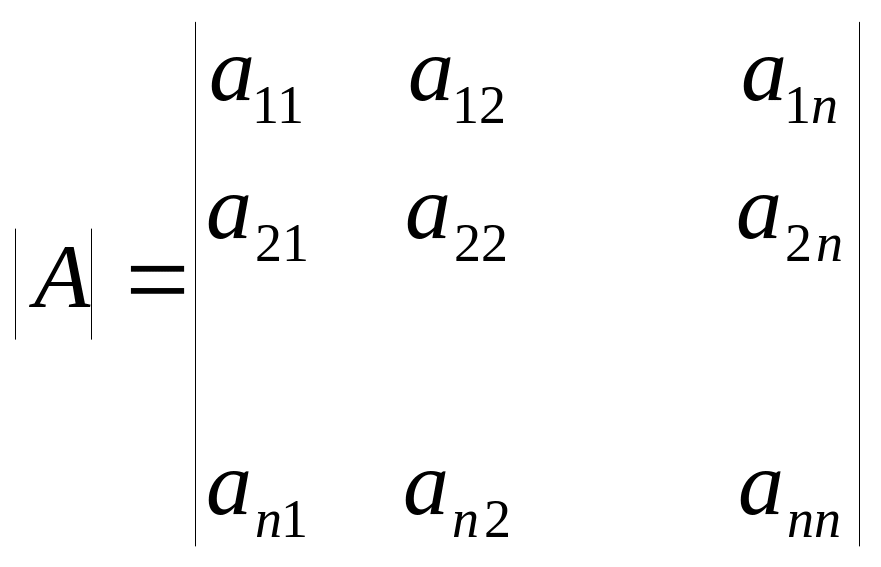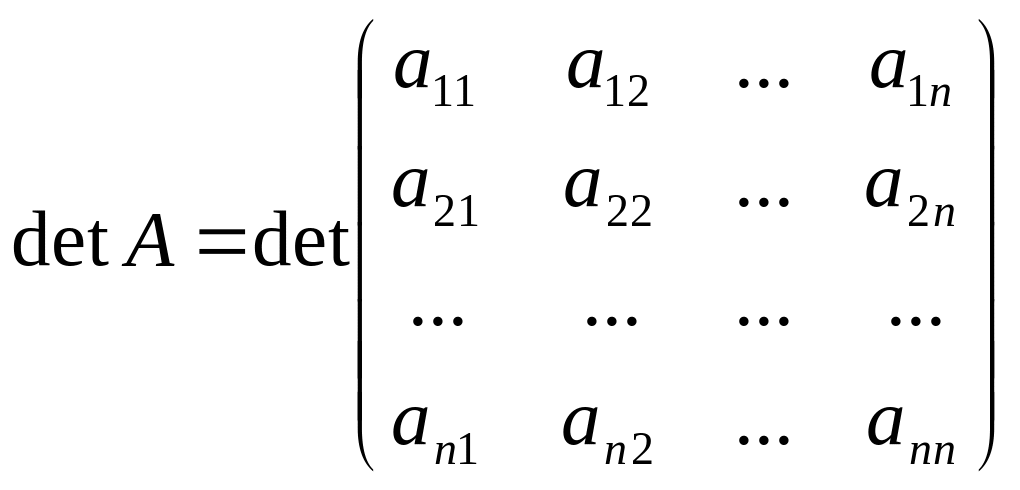Биологтарға арналған математика Қ.Оңайбаев

Биология мамандығына арналған математика

Әдебиеттер

1. С. Гроссман, Дж. Тернер. Математика для биологов (перевод с английского). М.: Высшая школа, 1983, 383 с.

2. В.С. Шипачев. Высшая математика (учебник для ВУЗ ов), М.: Высшая школа, 1998, 479 с.

3. В.С.Шипачев. Задачник по высшей математике. Мю: Высшая школа, 2003, 304 с.

4. А.А.Гусак. Высшая математика (учебное пособие для естественных специальностей университетов) том 1, Минск. : Издательство БГУ, 1983, 462 с.

5. А.А.Гусак. Высшая математика (учебное пособие для естественных специальностей университетов) том 2, Минск. : Издательство БГУ, 1984, 383 с.

6. А.П.Рябушко. Сборник индивидуальных заданий по высшей математике. Ч.1., Минск, Высшая школа 1990, 271 с.

7. А.П.Рябушко. Сборник индивидуальных заданий по высшей математике. Ч.2., Минск, Высшая школа 1991, 350 с.

8. А.П.Рябушко. Сборник индивидуальных заданий по высшей математике. Ч.3., Минск, Высшая школа 1991, 287 с.

9. П.Е.Данко, А.Г.Попов, Т.Я.Кожевникова Высшая математика в упражнениях и задачах. Ч.1. М.:Высшая школа, 1980, 320 с.

10. П.Е.Данко, А.Г.Попов, Т.Я.Кожевникова Высшая математика в упражнениях и задачах. Ч.2. М.:Высшая школа, 1986, 415 с.

Сызықтық алгебра элементтері

Матрица және оларға амалдар қолдану

Анықтама. Сандармен толтырылған тікбұрышты немесе квадрат таблицаны матрица деп атайды. Матрицадағы сандарды оның элементтері деп атайды.

Мысалдар

Матрицаның жолдары жоғарыдан төмен қарай 1 санынан (кейде 0 санынан) бастап номерленеді; Матрицаның бағандары солдан оңға қарай 1 санынан бастап номерленеді (кейде 0 санынан бастап номерленеді). Егер матрица элементінде екі номер тұрса оның біріншісі жолдың номерін, екіншісі бағанның номерін көрсетеді. Кейбе матрица бір ғана әріппен белгіленеді, мысалы сол жақтағы матрица тек A әрпімен белгіленіп тұр. Мұнда aij, i=1,2,…,m; j=1,2,…,n матрица элементтері. Бұл матрицаны кейде A=(aij) деп те белгілейді

Анықтама. m жолы және n бағаннан тұратын матрицаны mxn матрицасы деп атайды, немесе матрицаның реті mxn болады деп те айтады.

	Жоғарғы үшбұрышты матрица (бас диагональ асты ылғи ноль болады)
	Төменгі үшбұрышты матрица (қосымша диагональ үсті ылғи нольден тұрады)

Бас диагоналында тек қана бір саны орналасқан, қалған элементтері ылғи ноль болатын матрицаны бірлік матрица дейді де E арқылы белгілейді.

Барлық элементтері тек ноль болатын матрицаны нольдік матрица деп атайды.

Матрицаларға қолданылатын операциялар

Егер A матрицасының жолдарын сол номердегі бағанмен ауыстырса шыққан матрицаны берілген матрицаға транспонирленген матрица деп атап былай белгілейді AT.

Жолдары мен бағандарының сандары бірдей болатын A=(a_ij), B=(b_ij) матрицаларының қосындысы деп элементтері төмендегідей формуламен анықталатын C=(c_ij) матрицасын айтамыз.

Матрицалар қосындысы C=A+B деп белгіленеді.

Егер A=(a_ij) барлық элементтерін λ санына көбейтсек, онда осы операциядан алынған матрицаны A матрицасы мен λ санының көбейтіндісі дейміз.

λA=λ(a_ij)=(λa_ij), (i =1,2…,m ; j=1,2…,n ).

A=(a_ij) матрицасында m жол мен k баған болсын, ал B=(b_ij) матрицасында k жол мен n баған болсын. Элементтері төмендегі формуламен анықталатын m жолы мен n бағаны бар C=(c_ij) матрицасын A мен B матрицаларының көбейтіндісі деп атайды да C=AB деп белгілейді.

A матрицасындағы бағандардың саны B матрицасындағы жолдардың сандарына тең болғанда ғана A матрицасын B матрицасына көбейтуге болады.

1. Матрицаларды көбейту операциясы комутативті емес, яғни AхB мен BхA тең емес, тіпті олардың біреуін тапқанмен екіншісі анықталмаған болуы да мүмкін, басқаша айтқанда A мен B көбейтіндісін тапқанмен B мен A матрицаларын көбейтуге болмайтын болуы да мүмкін;

2. Кез-келген квадраттық матрицаны реті сондай болатын бірлік матрицаға көбейткенде матрица өзгермейді.

Жолдық матрицаны бағандық матрицаға көбейткенде шығатын санды скалярлық көбейтінді деп айтады.

Анықтауыштар

Әрбір квадраттық матрицаға оның анықтауышы деп аталатын санды сәйкестікке қоюға болады. Егер матрица A болса, оның анықтауышын |A| деп, немесе detA деп белгілейді.

Берілген матрица	Анықтауыштар

Біз төменде екінші және үшінші ретті квадраттық матрицалардың анықтауыштары қалай есептелетінін көрсетеміз. Жоғарғы ретті квадраттық матрицалардың анықтауышын есептеу күрделірек, бірақ MS Excel программасында оларды есептеуге арналған арнайы функция бар, оның көмегімен анықтауыштарды жылдам есептеуге болады.

Екінші ретті анықтауыштар төмендегі ережемен есептеледі:

Ережеден көрініп тұрғанындай екінші ретті анықтауыш бас диагоналдағы элементтердің көбейтіндісі мен қосымша диагоналдағы элементтердің көбейтіндісінің айырмасына тең болады екен.

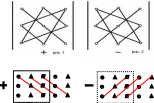Енді үшінші ретті квадраттық матрицаның анықтауышын есептеу ережесін (Саррюс ережесін) келтірелік:

Анықтама. mxn ретті A матрицасын қарастыралық. Осы матрицада кез-келген k жолы мен k бағанын алып солардың қиылысында тұрған элементтерден k ретті анықтауыш құралық. Осындай анықтауыштарды A матрицасының минорлары деп атайды. Нольге тең болмайтын минорлардың реттерінің ең үлкенін A матрицасының рангісі деп атайды да былай белгілейді: r(A).

Сызықтық алгебралық теңдеулер жүйесі

Төмендегідей сызықтық алгебралық теңдеулер жүйесін қарастыралық:

Жүйеде a_ij коэффициенттері мен b_j бос мүшелері берілген сандар. Жүйені матрицалық түрде AX=B деп жазуға болады. Мұнда А – жүйедегі белгісіздердің алдындағы коэффициенттерден тұратын матрица, B-бос мүшелерден тұратын бағандық матрица, X-белгісіздерден түратын бағандық матрица.