Нормальное (гаусса) распределение
Нормальным
называется распределение непрерывной
СВ
,
которое описывается плотностью
распределения
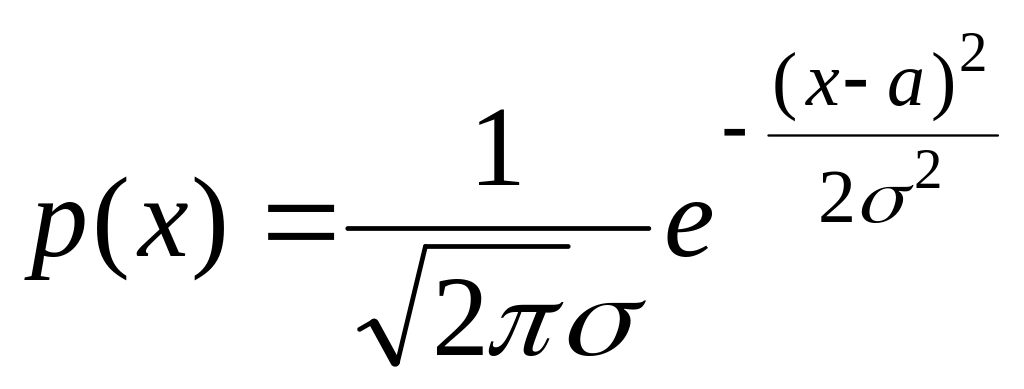
Вид нормальной кривой (Гаусса).
1.
Определена на
у>0
2. у>0
3 При х→∞ у→0
4. уmax=
при
х=а
5. Кривая симметрична относительно прямой х=а.
Гаусс Карл Фридрих
1777-1855
Немецкий математик, физик, астроном и геодезист.
Работы Гаусса оказали большое влияние на развитие высшей алгебры, теории чисел, дифференциальной геометрии, теории притяжения, классической теории электричества и магнетизма, геодезии, целых отраслей теоретической астрономии.
Астрономические работы в основном связаны с решением проблемы определения орбит малых планет и исследованием их возмущений. Гаусс разработал основной математический метод обработки неравноценных наблюдательных данных (метод наименьших квадратов).
Работы Гаусса по геодезии связаны с составлением детальной карты Ганноверского королевства; в результате теоретической разработки проблемы создал основы высшей геодезии
Гаусс первым всерьез занялся изучением земного магнетизма. Вместе с Вебером создал абсолютную систему электромагнитных единиц и сконструировал в 1833 первый в Германии электромагнитный телеграф. Единица напряженности магнитного поля названа Гауссом в его честь
Сформулировал ряд принципов теории вероятностей и математической статистики, включая распределение случайных величин вокруг среднего значения, получившее название распределения Гаусса.
Д
остаточно
знать параметры
,
чтобы задать нормальное распределение.
В
ес
20 «мисс Америка»
Возраст американских
президентов
коэффициент IQ у американцев
рост студентов
с
редний
балл
размер листьев
Какой вероятностный
смысл имеют параметры
и
?
Параметр – это матожидание СВ. Покажем это.
=
=
=
При этом мы учли,
что
- нечетная функция и
=0,
и то что интеграл Пуассона
.
Аналогично можно
показать, что
.
О
бщим
называют нормальное распределение с
прозвольными
и
.
Нормированным или стандартным называется
распределение при
=0
и
=1.
Плотность и функция стандартного нормального распределения :
φ(х)=
Ф(х)=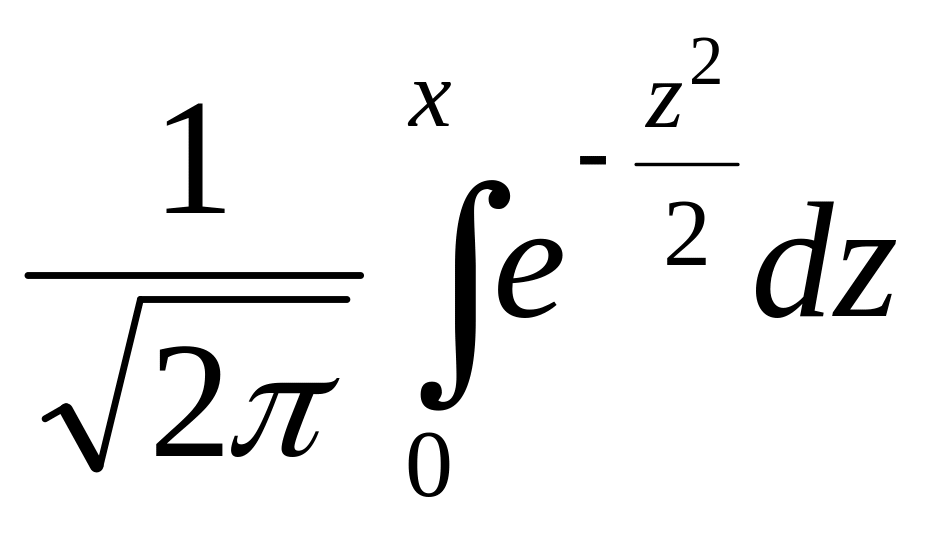
-функция
Лапласа
Эти функции затабулированы
Чтобы перейти от
общего к стандартному распределению
надо выполнить преобразование z=
.
Вероятность попадания св в заданный интервал
Для любой СВ: Р(α<х<β)=F(β)-F(α)
Для СВ, имеющей нормальное распределение:
P(α<х<β)=Ф(
)-Ф(
)
СВ
имеет нормальное распределение с
параметрами
=30,
=10.
Найти
.
=
Ф(
)-Ф(
)=Ф(
)-Ф(
)
=
= Ф(1)-Ф(-2)= Ф(1)+Ф(2)=0.34+0.48=0,82
Вероятность отклонения св от матожидания
Часто
требуется определить вероятность того,
что значения СВ не будут откланяться
от матожидания на заданную величину
:
=
=
СВ имеет нормальное распределение с параметрами =20, =10.
Найти
.
δ=3 =2Ф(
)
=2Ф(0.3)≈0.236.