
- •Краткий курс теории вероятностей
- •Часть 2. Случайные величины Определение случайной величины
- •Случайной величиной называется функция , определенная на пространстве элементарных исходов и принимающая действительные значения .
- •Свойства функции распределения
- •Дискретные случайные величины.
- •Числовые характеристики дискретных св
- •Прежде чем давать определения таких характеристик, рассмотрим простейшие действия над случайными величинами.
- •Математическое ожидание
- •Cвойства математического ожидания
- •Представим неслучайную величину в виде
- •Дисперсия
- •Свойства дисперсии
- •Некоторые распределения дискретных св Биномиальное распределение
- •Матожидание биномиального распределения.
- •Дисперсия биномиального распределения.
- •Аналогично нахождению матожидания получаем
- •Распределение Пуассона
- •Пуассон Симеон Дени
- •Геометрическое распределение
- •Дискретная св Непрерывная св
- •Свойства плотности распределения
- •Числовые характеристики непрерывных св.
- •Матожидание непрерывной св
- •2. Дисперсия непрерывной св
- •Равномерное распределение.
- •Матожидание равномерного распределения
- •Дисперсия равномерного распределения
- •Вероятность попадания св в заданный интервал:
- •Показательное распределение (экспоненциальное).
- •Вероятность попадания св в заданный интервал:
- •Матожидание и дисперсия показательного распределения
- •Cлучайный поток событий
- •Нормальное (гаусса) распределение
- •Вид нормальной кривой (Гаусса).
- •Гаусс Карл Фридрих
- •Вероятность попадания св в заданный интервал
- •Вероятность отклонения св от матожидания
- •Правило 3 сигм
Краткий курс теории вероятностей
и ВВЕДЕНИЕ В МАТЕМАТИЧЕСКУЮ СТАТИСТИКУ
Часть 2. Случайные величины Определение случайной величины
На всех предыдущих лекциях, рассматривая случайные события, мы практически ничего не говорили о числах. Попробуем разобраться с понятием случайной величины на пальцах.
Случайной величиной естественно назвать числовую величину, значение которой зависит от того, какой именно элементарный исход произойдет в результате опыта. Множество всех значений, которые случайная величина может принимать, называется множеством ее возможных значений. Следовательно, для задания случайной величины необходимо элементарным исходам поставить в соответствие числа.
Выбрасывание кости
Исходы |
|
|
|
|
|
|
Значение СВ |
1 |
2 |
3 |
4 |
5 |
6 |
Бросание дротика в мишень

Значение СВ – расстояние до центра
Случайной величиной называется функция , определенная на пространстве элементарных исходов и принимающая действительные значения .
Случайные величины бывают дискретные и непрерывные. Дискретные: число очков на костяшке домино, число бросаний монеты до первого герба, оценка студента на экзамене. Непрерывные: погрешность измерения, время до отказа прибора, время опоздания на лекцию.
Функция распределения СВ.
Для исследования вероятностных свойств СВ необходимо знать правило, позволяющее находить вероятность того, что СВ примет определенное значение. Такое правило называется законом распределения СВ.
Введем понятие функции распределения СВ. Пусть х – число. СВ принимает значения, которые могут быть больше или меньше этого числа.
Функцией
распределения
![]() называется функция, равная вероятности
того, что СВ
примет значение, меньшее х :
называется функция, равная вероятности
того, что СВ
примет значение, меньшее х :![]() .
.
![]() пробегает все
значения от
пробегает все
значения от
![]() до
до
![]() .
Геометрически - вероятность того, что
случайная величина примет
значения, меньшие
:
.
Геометрически - вероятность того, что
случайная величина примет
значения, меньшие
:

Понятно, что чем
больше х, тем больше вероятность
![]() .
.
Дискретная СВ
![]() ,
принимающая 2 значения:
,
принимающая 2 значения:
-
Значение
0
1
Вероятность
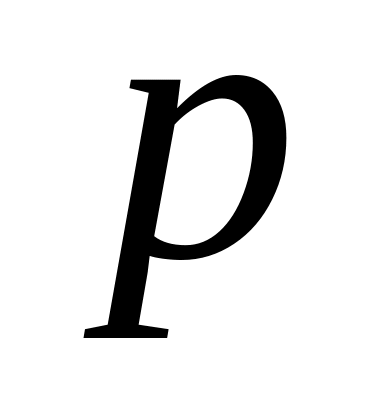


F(-5)=P(X<-5) =0
F(-2)=P(X<-2)=0
F(5)=P(X<5)x=1
Свойства функции распределения
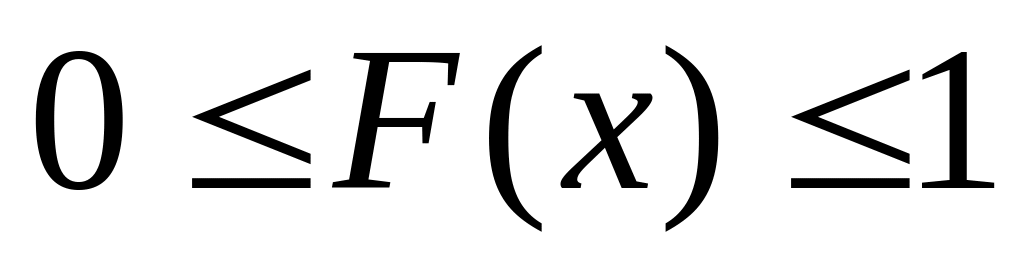 ,
т.к. F(x)=вероятности.
,
т.к. F(x)=вероятности.
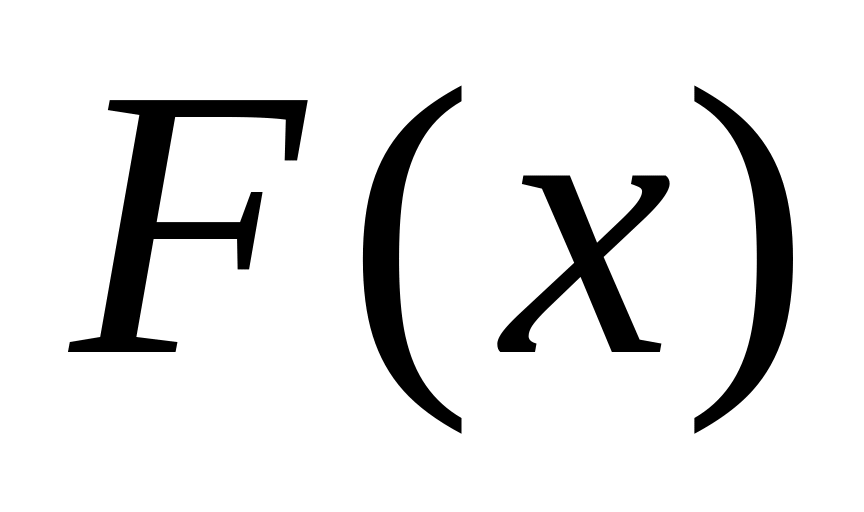 -
неубывающая функция, т.е. из х1<x2
-
неубывающая функция, т.е. из х1<x2
 F(x1)≤F(x2).
F(x1)≤F(x2).
Доказательство.
Пусть х2>x1. Событие, состоящее в том, что СВ Х примет значение меньшее х2, можно разделить на два несовместимых события
А1: примет значения < x1 с вероятностью P( <x1);
А2: х1≤ значение < x2 с вероятностью P(x1≤ <x2).
По теореме сложения несовместных событий
P(x<x2)= P(А1+А2)=P(x<x1)+P(x1≤x<x2).
Отсюда P(x<x2)-P(x<x1)=P(x1≤x<x2) и
* F(x2)-F(x1)=P(x1≤x<x2)≥0,
след. - неубывающая функция.
Следствие.
Вероятность того,
что СВ примет значение, заключенное в
интервале
![]() равна приращению функции распределения
на этом интервале:
равна приращению функции распределения
на этом интервале:
![]() .
.
 P(x<∞)
P(x<∞)
![]() P(x<-∞)
P(x<-∞)
непрерывна слева:
lim F(x)=F(a)
x→a-0
