3.3. Анализ качества построенной модели

Построение эмпирического уравнения множественной линейной регрессии является начальным этапом эконометрического анализа. Следующей важнейшей задачей является проверка качества регрессионной модели, которая осуществляется по следующим основным направлениям:

 анализ точности и статистической значимости коэффициентов уравнения регрессии (параметров модели),

 проверка общего качества уравнения регрессии.

Указанная схема проверки применима для классической нормальной модели множественной регрессии и отражена во многих компьютерных пакетах, решающих задачи эконометрики.

Для анализа качества построенной модели необходимо знание соответствующих дисперсий и стандартных ошибок, что позволяет вычислять характеристики точности оценок, строить доверительные интервалы для теоретических коэффициентов, проверять соответствующие гипотезы.

Из рассмотрения матрицы ковариаций вектора случайных отклонений V(е) следует выражение:

. (3.18)

Равенство (3.18) означает, что несмещенной оценкой случайных отклонений является выборочная дисперсия остатков S², которая определяется по формуле:

. (3.19)

Формула (3.19) легко объяснима, так как показывает, что в случае множественной регрессии теряется m + 1 степеней свободы при определении k = m + 1 неизвестных параметров, а не две (n  2), как в случае парной регрессии. Можно сказать, что сумма квадратов остатков всегда определяет оценку дисперсии случайных отклонений с учетом поправочного коэффициента, зависящего от числа степеней свободы.

Аналогично парной регрессии характеристика

(3.20)

называется стандартной ошибкой регрессии.

3.3.1. Анализ точности и статистической значимости коэффициентов уравнения множественной регрессии

Числовыми характеристиками точности коэффициентов множественной регрессии (параметров модели) , являются их средние квадратические отклонения (стандартные ошибки) , величина которых прямо пропорциональна S.

Можно показать, что матрица ковариаций вектора параметров модели В (матричный аналог дисперсии) может быть представлена в виде:

. (3.21)

Напомним, что ковариация двух переменных характеризует как степень рассеяния относительно их математических ожиданий, так и взаимосвязь этих переменных. При выполнении предпосылок МНК математическое ожидание .

Рассматривая матрицу ковариаций V(B) с элементами σ_ij, можно заметить, что на ее главной диагонали находятся дисперсии оценок параметров модели, т. е. . Тогда для выборочных дисперсий эмпирических коэффициентов справедливо выражение:

(3.22)

где – выборочная дисперсия случайных отклонений (остатков); – диагональный элемент матрицы (Х^ТХ)^1.

Стандартная ошибка j-го коэффициента регрессии будет определяться по формуле:

(3.23)

Таким образом, с помощью обратной матрицы (Х^ТХ)^1 определяется не только сам вектор оценок параметров (3.17), но и стандартные ошибки его компонент [25,28].

В частности, для модели с двумя объясняющими переменными (факторами) стандартные ошибки вычисляются по следующим формулам:

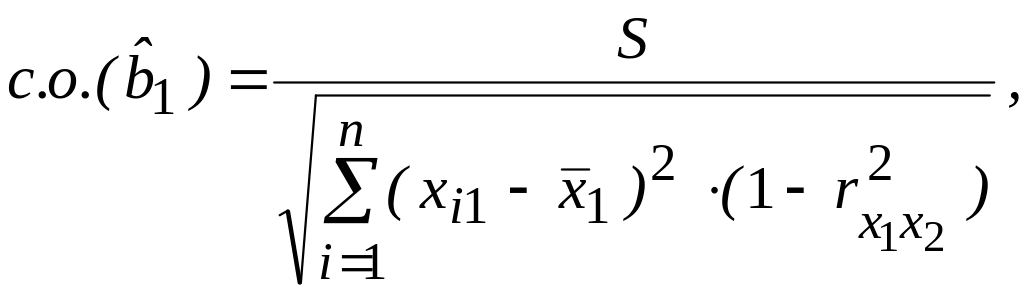(3.24)

,

где – выборочный коэффициент корреляции между объясняющими переменными Х₁ и Х₂.

Из формул (3.24) следует, что стандартные ошибки тем меньше, чем меньше степень взаимного влияния факторов-аргументов, определяемая значением .

Рассчитав стандартные ошибки коэффициентов множественной линейной регрессии, можно приступать к проверке статистической значимости этих коэффициентов (параметров модели). Как и в случае парной регрессии, эта задача решается по схеме статистической проверки гипотез. Используется статистика которая имеет в данной ситуации распределение Стьюдента с числом степеней свободы v = n  m  1 (n – объем выборки, m – число объясняющих переменных в модели). При требуемом уровне значимости  наблюдаемое значение t-статистики сравнивается с критической точкой t_{, n  m  1} распределения Стьюдента.

Если установлено, что |t_набл| > t_кр, то коэффициент считается статистически значимым. В случае, когда |t_набл|  t_кр коэффициент считается статистически незначимым (статистически близким к нулю). Это означает, что фактор-аргумент Х_j не обладает существенной линейной связью с исследуемой переменной Y. Другими словами, этот фактор не оказывает заметного влияния на результирующий экономический показатель и лишь искажает реальную картину взаимосвязи.

Формально, после установления факта статистической незначимости коэффициента , следует исключить из уравнения регрессии переменную Х_j, что упрощает модель и делает ее более конкретной. Однако в эконометрических исследованиях вопрос об исключении из уравнения модели незначимых переменных не должен решаться столь однозначно. Окончательное решение должно быть принято после тщательного качественного анализа.

Надежность полученных оценок также определяется доверительными интервалами для параметров модели. Если учесть, что относительная величина 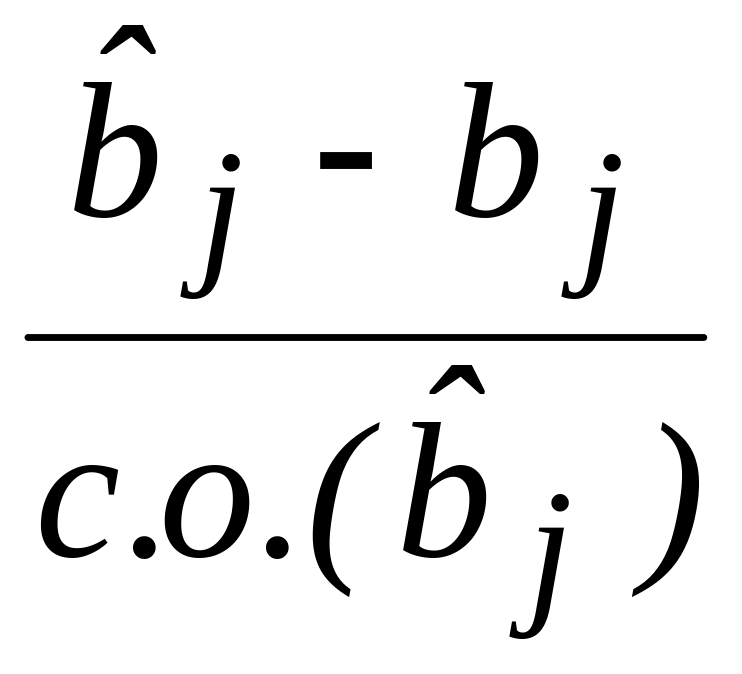имеет распределение Стьюдента, и выполняется условие (t_{, n  m  1} определяется по таблице критических точек распределения Стьюдента), то доверительный интервал, накрывающий с надежностью (1  ) неизвестное значение теоретического параметра b_j, определяется неравенством:

. (3.25)

Аналогично парной регрессии (см. раздел 2.5) может быть построена интервальная оценка для индивидуальных значений зависимой переменной у₀ при заданном векторе аргументов Х₀:

(3.26)

где – средняя квадратическая ошибка рассчитанных по модели (прогнозируемых) значений , записанная в матричной форме.