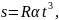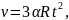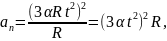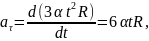1) У точек находящихся на колесе и лежащих на радиусе, будут одинаковы угловые скорости. Используем связь угловой и линейной скоростей:

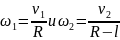
т.к. ω₁=ω₂, приравниваем правые части уравнений:

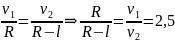
Решим уравнение относительно R:

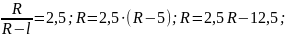
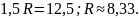
Ответ: Радиус вращающегося колеса равен 8,33 см.

Пример 13. На рис.28 показаны направления вращения гироскопа (волчка) и указано, увеличивается или уменьшается угловая скорость. Укажите номер рисунка, на котором правильно указано направление углового ускорения.

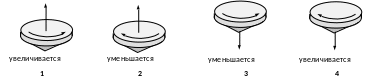
Рис.28

Решение. Псевдовектор угловой скорости связан с направлением вращения правилом буравчика (правого винта). На рис.28.1 и рис.28.3 он направлен вверх, на рис.28.2 и рис.28.4 - вниз.

При возрастании угловой скорости ее приращение, а соответственно и вектор углового ускорения совпадают с вектором угловой скорости (рисунки 1 и 4). При уменьшении угловой скорости ее приращение, а соответственно и вектор углового ускорения противоположны вектору угловой скорости (рис.28.2 и рис.28.3). Следовательно, на всех рисунках направление углового ускорения указано правильно.

Пример 14. Опишите движение вращающегося твердого тела в случаях, когда угловая скорость изменяется согласно графикам 1 и 2, изображенным на рис.29.

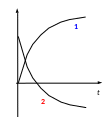
Рис.29

Решение. Начнем с того, что вращение бывает в двух направлениях - по часовой стрелке и против. С направлением вращения связан псевдовектор угла поворота и угловой скорости. Пусть положительным будем считать направление вращения по часовой стрелке.

Для движения 1 угловая скорость возрастает, но угловое ускорение ε=dω/dt (производная) уменьшается, оставаясь положительным. Следовательно, это движение является ускоренным по часовой стрелке с уменьшающимся по величине ускорением.

Для движения 2 угловая скорость уменьшается, затем достигает в точке пересечения с осью абсцисс нуля, а далее становится отрицательной и возрастает по модулю. Угловое ускорение (вспомните геометрический смысл производной) отрицательно и уменьшается по модулю. Таким образом, сначала точка двигалась по часовой стрелке замедленно с уменьшающимся по модулю угловым ускорением, остановилась и стала вращаться ускоренно с уменьшающимся по модулю ускорением (оба вектора - и угловая скорость, и угловое ускорение направлены в одну сторону).

Пример 15. Скорость точки, движущейся по кривой, уменьшается по модулю. На каком рисунке, показанных на рис.30 правильно показан вектор полного ускорения?

Рис.30

Решение. При движении по криволинейной траектории скорость изменяется по величине и направлению. Составляющая ускорения, характеризующая быстроту изменения скорости по величине, называется тангенциальным ускорением. Она связана с приращением вектора скорости, направленным по касательной к траектории, как и сама скорость. При ускоренном движении тангенциальная составляющая совпадает с вектором скорости, при замедленном - противоположна (как на рис.30.1)

Составляющая ускорения, характеризующая быстроту изменения скорости по направлению, называется нормальным ускорением. Она связана с приращением вектора скорости, направленным перпендикулярно касательной к траектории. Нормальное ускорение всегда направлено к центру кривизны траектории (как на рис. 30.3)

Вектор полного ускорения 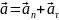правильно изображен на рис.30.2.

Пример 16. Угловая скорость точки, движущейся по окружности, изменяется по графику, изображенному на рис.31. Как изменяется со временем угол между векторами ускорения и скорости?

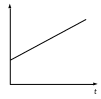
Рис.31

Решение. Согласно графику угловая скорость линейно возрастает. Угловое ускорение по определению равно производной угловой скорости по времени ε=dω/dt.

Производная линейной функции постоянна, поэтому угловое ускорение не изменяется.

Запишем выражения, связывающие составляющие ускорения с угловыми величинами:

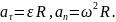
Следовательно, тангенциальное ускорение не изменяется по величине в процессе движения, а нормальное ускорение возрастает.

Построим векторы скорости, нормального, тангенциального и полного ускорений. Вектор скорости направлен по касательной к траектории. Направление вектора ускорения рассматривалось ранее.

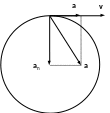
Рис.32

Из рис.32 видно, что угол α между векторами скорости и ускорения возрастает.

Пример 17. Точка движется, замедляясь, по окружности радиуса R так, что в каждый момент времени ее тангенциальное и нормальное ускорения по модулю равны друг другу. В начальный момент времени t = 0 скорость точки равна v₀. Найти скорость и ускорение точки как функцию времени.

Решение. Установим уравнения, связывающие а_n и а_τ. По условию задачи модули нормального и тангенциального ускорений совпадают: |a_n|=|a_τ|. Нормальное ускорение всегда положительно. При замедленном движении приращение скорости отрицательно. С учетом этих замечаний система уравнений принимает вид

а_n=-а_τ, (1)

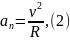
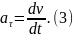
Подставляя (2) и (3) в (1), приходим к уравнению с разделяющимися переменными:

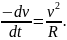
Разделяя переменные v и t, получаем

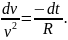
Интегрируем в пределах от t = 0, v = v₀ до t и v(t)

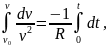
в результате имеем:

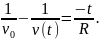
Из этого соотношения находим искомую зависимость скорости от времени

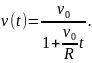
Подставляем v(t) в формулу (2)

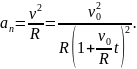
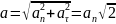Учитывая, что a_n=-a_τ и , получаем зависимость полного ускорения от времени:

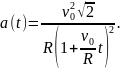
Пример 18. Материальная точка движется по окружности радиуса R так, что зависимость угла поворота от времени задана уравнением φ=αt³. Найти полное ускорение точки как функцию времени.

Решение. Решим задачу двумя способами.

1 способ. Выпишем формулы соответствующие данному способу.

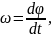
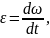
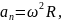
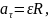
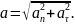
Выполним указанные в формулах математические действия.

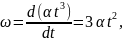
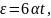
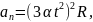
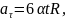
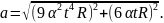
2 способ. Выпишем формулы соответствующие данному способу.

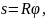
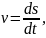
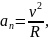
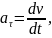
Выполним указанные в формулах математические действия.