Вращение тела вокруг неподвижной точки

Название такого вида движения довольно точно его определяет. Часто это движение называют сферическим движением потому, что все точки тела движутся по сферическим поверхностям.

Наглядным примером такого движения является волчок, закономерности движения которого лежат в основе гироскопических приборов.

1) Углы Эйлера. Уравнения вращения тела с одной неподвижной точкой.

Рис. 9.5.

Рис. 9.5.

Положение тела определяется тремя углами. Используются различ­ные системы углов. Например, кора­бельные углы, самолётные углы и др. Но самыми распространёнными яв­ляются углы Эйлера: Ψ (пси), 𝜃(тета), φ (фи).

Положение тела опре­деляется следующим образом. На­значаются две системы декартовых осей. Первая система – неподвижные оси x,y,z. На­чало которых берётся в неподвижной точке O тела (рис. 16). Вторая сис­тема, оси x₁, y₁, z₁, связывается с телом. Поэтому положение тела будет опреде­ляться как положение этих осей относи­тельно неподвиж­ных.

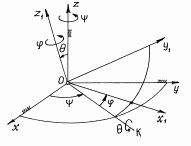
Рис.16

Рис. 9.4.

Рис. 9.5.

Когда углы Эйлера равны нулю, под­вижные оси совпадают с непод­вижными. Чтобы опреде­лить положение тела, соот­ветст­вующее заданным углам Эйлера, производим следующие действия. Сначала подвижные оси, а значит и тело, поворачи­ваем на угол Ψ вокруг оси z. При этом оси x₁ и y₁ отойдут от осей x и y в гори­зон­тальной плоскости и ось x₁ займёт по­ложение OK (рис.16). Затем тело вращаем вокруг но­вого поло­жения оси x₁ (прямой OK) на угол θ. Ось z₁ отойдёт от оси z на этот угол θ, а ось y₁ приподнимется над горизонтальной плоскостью. Наконец, тело (и подвижные оси) вращаем вокруг нового положения оси z₁ на угол φ. Ось x₁ отойдёт от положения OK в на­клонной плоскости, перпендикуляр­ной оси z₁. Это положение тела и будет соответствовать углам Эйлера (на рисунке само тело не пока­зано).

Линия пересечения неподвижной плоскости xOy и подвижной x₁Oy₁, прямая OK, называ­ется линией узлов. Угол Ψ называется углом прецессии, угол θ – углом нутации, угол φ – углом собственного вращения. Эти названия углов пришли из теории гироскопов.

При движении тела углы Эйлера изменя­ются по определённым законам Ψ=Ψ(t); θ=θ(t); φ=φ(t) которые называются уравнениями вра­щения.

На примере вращающегося волчка можно лучше разобраться в этих углах Эйлера (рис.17). Ось волчка z₁ описывает конус вокруг неподвижной оси z. Это вращение определяется углом Ψ (говорят: волчок совершает прецессию). Отклонение оси волчка от вертикали – угол нутации θ.

А вращение волчка вокруг своей оси z₁, определяемое углом φ – собственное вращение.

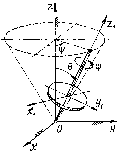
Рис.17

2) Теорема Даламбера – Эйлера. Мгновенная ось вращения.

Проведём в теле сферическую поверх­ность произвольного радиуса с центром в неподвижной точке O (рис.18).

Рис.18

По­кажем у тела какие-нибудь две точки A и B, расположенные на этой сфере. Со­единим их по сфере дугой наибольшего радиуса (кратчайшее расстояние между точками). Переместим тело в новое по­ло­жение. Точки, а значит и дуга, займут по­ложение A₁ и B₁. Соединим точки A и A₁, B и B₁ дугами большого радиуса AA₁ и BB₁. Посередине этих дуг прове­дём им перпендикулярные дуги и най­дём их точку пересечения P₁. Соединим эту точку P₁ с точками A, B, A₁, B₁. Получим два сфе­рических треугольника ∆ABP₁ и ∆A₁B₁P₁, расположенных на этой сфере. Эти два треугольника равны, как треугольники с равными сторонами (AB=A₁B₁, а AP₁=A₁P₁ и BP₁=B₁P₁ – как дуги равноудалённые от пер­пендикуляров). Так как эти два треугольника расположены на одной сфере и имеют общую вершину P₁, то их можно совместить поворотом сферы, а значит и тела, вокруг прямой OP₁.

Поэтому можно сделать вывод, что тело с одной неподвижной точкой можно переместить из одного положения в другое поворотом вокруг некоторой оси, проходящей через не­подвижную точку O. Это утверждение – есть теорема Даламбера-Эйлера.

Рис. 9.7.

Конечно, такое перемещение не яв­ля­ется истинным движением тела. На самом деле тело переходило из первого положе­ния в другое каким-то другим, наверное бо­лее сложным путём. Но, если время ∆t такого пере­хода мало, то это перемещение будет близко к действительному. А при ∆t→0 можно предположить, что для данного момента времени тело поворачива­ется вокруг некоторой оси Р, проходя­щей через неподвижную точку O, вращаясь вокруг неё с угловой скоро­стью . Конечно, для каждого дру­гого момента времени эта ось рас­поло­жена иначе. Поэтому ось P называют мгновенной осью вращения, а угло­вую скорость – мгновенной угловой скоростью, вектор которой на­прав­лен по оси.

Рис. 9.8.