5.Расчет на действие снеговой нагрузки
Указываем схему приложения и величину нагрузки: (рис. 3.5,а):
Ps = 191,52 кН; Ms2 = 52,67 кНм.
Рассматриваем отдельную стойку, находящуюся под воздействием сосредоточенного момента (см. рис. 3.4,б). Определяем опорные реакции верха стойки по формулам из таблицы (коэффициенты M, R – из п. 3.4):
Определяем ординаты грузовой эпюры моментов в характерных сечениях колонны:
М1 = ММ = 11,22 кН м;
М21 = ММ – RMНв = 11,219 – 5,0045,75 = -17,55 кН м;
М23 = ММ – RMНв + Мs2= 11,219 – 5,0045,75 + 52,67 = 35,12 кН м;
М3 = ММ – RMН + Мs2 = 11,219 – 5,00415,20 + 52,67 = -12,17 кН м.
Момент на опоре
ригеля:
Момент в середине
пролёта ригеля:
Найденные ординаты откладываем на стойках и ригеле рамы, в результате получаем грузовую эпюру моментов Мр в О.С.М.П. (см. рис. 3.4,в).
Рассматривая равновесие верхнего узла рамы, находим реакцию в наложенной связи R1p от воздействия снеговой нагрузки (рис. 3.5,б):
R1p = - (M1 + M0) = - (11,22 + 766,08) = -777,30 кН.
Из решения канонического уравнения находим неизвестное перемещение:
Вычисляем ординаты окончательной эпюры моментов, используя формулу:
М1 = -341,730,332 + 11,22 = -102,23 кНм;
М21 = -80,030,332 – 17,55 = -44,12 кНм;
М23 = -80,030,332 + 35,12 = 8,55 кНм;
М3 = 350,070,332 – 12,17 =104,05 кНм;
М0 = 20000,332 – 766,08 = -102,08 кНм;
Мr = 20000,332 + 383,04 = 1047,04 кНм.
По найденным значениям строим окончательную эпюру моментов М, кНм (рис. 3.5,в).
Проверкой правильности построения эпюры является соблюдение условий равновесия узла рамы: М0 = М1.
Проверка выполняется: 102,08 102,23 кНм.
Строим эпюру поперечных сил Q в раме (рис. 3.5,г).
Максимальная поперечная сила возникает на опоре ригеля:
Q0 = Ps = 191,52 кН.
Поперечные силы на уровне верха и низа колонны:
Проверка: Q1 = Q3 = 10,11 кН. Проверка выполняется.
а)
б)
в)
г)
д)
Рис.3.5. Расчёт на действие снеговой нагрузки.
Строим эпюру продольных сил N в раме (рис. 3.5,д).
В ригеле Nr = Q1 = 10,11 кН.
В стойках N1 = Ps = 191,52 кН.
6.Расчёт на действие ветровой нагрузки
Указываем схему приложения и величину нагрузки (рис.3.6,а):
we,a = 2,578 кН/м; Pw,a = 10,674 кН;
we,p = 1,934 кН/м; Pw,p = 8,005 кН.
Определяем опорные реакции верха стоек:
Вычисляем ординаты грузовой эпюры моментов в стойках рамы (рис. 3.6,б).
Левая стойка:
М1,а = -34,65 кНм;
М2,а = -34,649 + 17,3655,75 – 0,52,578(5,75)2 = 22,58 кНм;
М3,а = -34,649 + 17,36515,20 – 0,52,578(15,20)2 = -68,51 кНм.
Правая стойка:
М1,р = -25,99 кНм;
М2,р = -25,993 + 13,0275,75 – 0,51,934(5,75)2 = 16,94 кНм;
М3,р = -25,993 + 13,02715,20 – 0,51,934(15,20)2 = -51,40 кНм.
По найденным значениям строим грузовую эпюру моментов Мр в О.С.М.П. (рис.3.6,в).
Из уравнения равновесия ригеля рамы находим реакцию в наложенной связи R1,p. (рис.3.6,г):
R1,p = -(Rw,a + Rw,p + Pw,a + Pw,p) = - (17,365 + 13,027 + 10,674 + 8,005) = -49,071 кН.
Находим неизвестное перемещение из решения канонического уравнения:
Вычисляем ординаты окончательной эпюры моментов, используя формулу:
Левая стойка:
М1,а = 45,5132,430 – 34,65 = 75,95 кНм;
М2,а = -12,5452,430 + 22,58 = -7,90 кНм;
М3,а = -107,9612,430 – 68,51 = -330,86 кНм.
Правая стойка:
М1,р = 45,5132,430 – 25,99 = 84,61 кНм;
М2,р = -12,5452,430 + 16,94 = -13,54 кНм;
М3,р = -107,9612,430 – 51,40 = -313,75 кНм.
Окончательная эпюра моментов М, кНм показана на рис. 3.6, д.
Рис.
3.6. Расчёт на действие ветровой
нагрузки
Ординаты эпюры поперечных сил Q находим, рассматривая равновесие стоек рамы (рис.3.6,е):
Левая стойка:
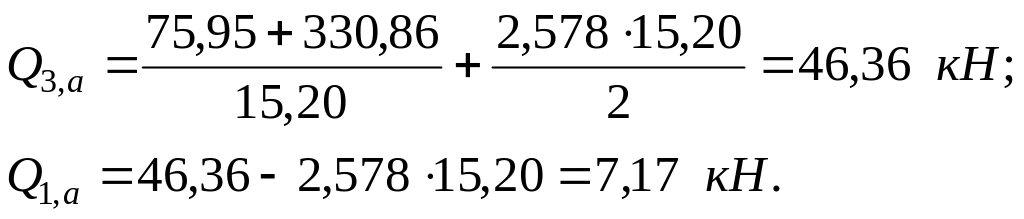
Правая стойка:
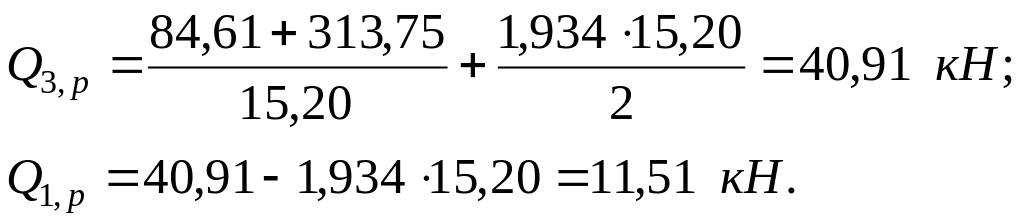
По найденным значениям строим эпюру поперечных сил Q, кН (рис.3.6,ж).
Строим эпюру продольных усилий N в ригеле, рассматривая равновесие верхних узлов рамы (рис.3.6, и):
Левый узел: Nr,a = Q1,a – Pw,a = 7,17 – 10,674 = -3,50 кН;
Правый узел: Nr,p = - Q1,p + Pw,p = -11,51 + 8,005 = -3,50 кН.
Проверка: Nr,a = Nr,p. Проверка выполняется.
Выполним общую проверку равновесия рамы, заменив опорные связи их реакциями (рис.3.12,к):
Σx = 0: Q3,a + Q3,p - H(we,a + we,p) – Pw,a – Pw,p = 0;
46,36 + 40,91 – 15,20(2,578 + 1,934) – 10,674 – 8,005 = 0,009; 0,0090.
Условие равновесия выполняется.