35

3. Статический расчёт поперечной рамы

1.О

(для жёсткого сопряжения ригеля с колонной)

сновные положения расчёта

Выбор метода расчёта

Поперечная рама каркаса является статически неопределимой системой. При расчёте будем пользоваться методом перемещений с использованием таблиц для стержней ступенчато-переменной жёсткости (прил. 4).

Выбор основной системы

В рамах с жёстким сопряжением ригеля с колонной два неизвестных: горизонтальное смещение ригеля ∆ и углы поворота φ жестких узлов рамы (в силу симметрии рамы углы можно принять одинаковыми). Чтобы не рассчитывать систему с двумя неизвестными, используем два упрощения:

• при действии вертикальных симметрично приложенных нагрузок (постоянной, снеговой) принимаем, что горизонтальных смещений ригеля не происходит, тогда неизвестными будут только углы поворота его узлов φ.

• при действии несимметрично приложенных нагрузок (ветровая, крановая) ригель принимаем абсолютно жестким, тогда неизвестным будет только его горизонтальное смещение ∆.

Геометрические характеристики

Задаём соотношения моментов инерции сечений элементов рамы: нижней части колонны J_н, верхней части колонны J_в, ригеля рамы J_r.

Принимаем J_н / J_в = 6; J_r / J_н = 4 (обычно J_н / J_в = 5…10; J_r / J_н = 2…6; чем выше грузоподъёмность крана, тем больше эти соотношения)

Зададим условную жесткость верхнего участка стойки EJ_в = 1000 EJ.

Т огда из принятых соотношений получим: EJ_н = 6 000 EJ, EJ_r = 24 000 EJ.

В 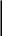ычислим параметры, участвующие в расчётных формулах таблицы:

А = 1 + α μ = 1 + 0,378  5 = 2,890;

В = 1 + α² μ = 1 + (0,378)²  5 = 1,714;

С = 1 + α³ μ = 1 + (0,378)³  5 = 1,270;

D

Рис. 3.1. Расчётные сечения и правило знаков.

= 1 + α⁴ μ = 1 + (0,378)⁴  5 = 1,102;

К = 4АС – 3В² = 42,8901,270 – 3(1,714)² = 5,868.

Расчётные сечения и правило знаков

Внутренние усилия будем определять в характерных сечениях колонны, располагающихся соответственно по концам её верхнего и нижнего участков. Всего рассматривается 4 сечения, которые обозначаются 1-1, 2-2, 3-3, 4-4 (рис.3.1).

Внутренним усилиям, возникающим на уровне верха, уступа и низа колонны присвоим соответственно индексы 1,2,3 (например, М₂).

Усилия в точке 2, действующие выше уступа (т.е. в начале участка 2-1), будем обозначать индексом 21 (например, М₂₁); действующие ниже уступа – индексом 23 (например, М₂₃).

Знаки внутренних усилий определяются по правилам строительной механики:

М - откладывается со стороны растянутого волокна стержня;

Q - положительная, если вращает стержень по часовой стрелке;

N - положительная, если вызывает растяжение стержня.

Для изгибающих моментов установим условное правило знаков: «+», если эпюра отложена справа от стержня, и «–», если слева (см. рис. 3.1).

2.Учёт пространственной работы каркаса здания

Для учёта пространственной работы используем коэффициент пространственной работы каркаса α_р, на который умножаем перемещение рамы z, найденное в результате решения канонического уравнения метода перемещений:

z_pr = z  α_р, α_р < 1,0.

В данном проекте принята конструкция покрытия с использованием прогонов, поэтому коэффициент α_рr находим по формуле:

,

где

n – число колёс кранов на одном пути; от двух кранов n = 8;

Σy – сумма ординат линии влияния опорной реакции подкрановой балки: Σy = 4,968;

β	α	α′
0,01	0,77	0,20
0,02	0,73	0,22
0,03	0,71	0,24
0,04	0,69	0,25
0,05	0,67	0,25
0,10	0,62	0,26
0,15	0,58	0,26
0,20	0,56	0,26
0,50	0,46	0,25

α, α′ – коэффициенты, определяемые по справочной таблице в зависимости от параметра ,

где l – шаг поперечных рам: l = 12 м;

H – высота колонны: H = 15,20 м;

m – отношение момента инерции нижней части колонны к суммарному моменту инерции горизонтальных связевых элементов; обычно принимается в пределах m = 0,5…0,25; примем m = 0,3;

d – коэффициент приведения ступенчатой колонны к колонне постоянного сечения, эквивалентной по смещению; принимается в зависимости от вида сопряжения ригеля с колонной; при жёстком сопряжении d = 1/K = 1/5,868 = 0,170.

Т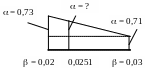 огда