Контрольные вопросы и задания

1 . По изображенным многоугольникам сил (рис. 2.7) решите, сколько сил входит в каждую систему и какая из них уравновешена. (Обратить внимание на направление векторов.)

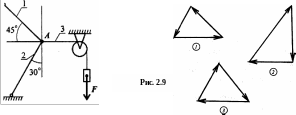
2 . Из представленных силовых треугольников выберете тре­угольник, построенный для точки А (рис. 2.8, 2.9).

4. Ш ар подвешен на нити и находится в равновесии. Обратить внимание на направление реакции от гладкой опоры и условие равновесия шара (рис. 2.8).

5. Груз F подвешен на канате и находится в равновесии. Обратить внимание на реакции, приложенные к точке А. Силы, не приложенные к точке А, не рассматриваются. Не забывать об условии равновесия системы сил (рис. 2.9).

Лекция 3 Тема 1.2. Плоская система сходящихся сил. Определение равнодействующей аналитическим способом

Знать аналитический способ определения равнодействующей силы, условия равновесия плоской сходящейся системы сил в ана­литической форме.

Уметь определять проекции силы на две взаимно перпендику­лярные оси, решать задачи на равновесие в аналитической форме.

Проекция силы на ось

Проекция силы на ось определяется отрезком оси, отсекаемым перпендикулярами, опущенными на ось из начала и конца вектора (рис. 3.1).

Величина проекции силы на ось равна произведению модуля си­лы на косинус угла между вектором силы и положительным направ­лением оси. Таким образом, проекция имеет знак: положительный при одинаковом направлении вектора силы и оси и отрицательный при направлении в сторону отрицательной полуоси (рис. 3.2).

F_1x = F₁ cos α₁ > 0; F_2x = F₂ cos α₂ = - F₂ cos β₂;

cos α₂ = cos (180° — β₂) = — cos β₂

F_3x = F₃ cos90° = 0; F_4x = F₄ cos180° = - F₄.

Проекция силы на две взаимно перпендикулярные оси (рис. 3.3).

Определение равнодействующей системы сил аналитическим способом

Величина равнодействующей равна векторной (геометрической) сумме векторов системы сил. Определяем равнодействующую геометрическим способом.

Выберем систему координат, определим пропорции всех заданных векторов на эти оси (рис. 3.4, а).

Складываем проекции всех векторов на оси х и у (рис. 3.4, б).

М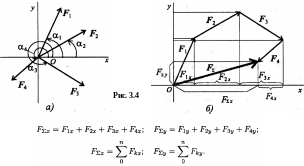 одуль (величину) равнодействующей можно найти по известным проекциям:

Н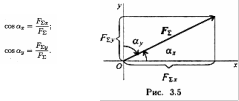 аправление вектора равнодействующей можно определить по величинам и знакам косинусов углов, образуемых равнодействующей с осями координат (рис. 3.5).

Условия равновесия плоской системы сходящихся сил в аналитической форме

И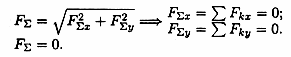 сходя из того, что равнодействующая равна нулю, получим:

Условия равновесия в аналитической форме можно сформули­ровать следующим образом:

Плоская система сходящихся сил находится в равновесии, ес­ли алгебраическая сумма проекций всех сил системы на любую ось равна нулю.

Система уравнений равновесия плоской сходящейся системы сил:

В задачах координатные оси выбирают так, чтобы решение было наиболее простым. Желательно, чтобы хотя бы одна неизвестная сила совпадала с осью координат.

Примеры решения задач

Пример 1. Определить величины и знаки проекций представленных на рис. 3.6 сил.

Решение

Пример 2. Определить величину и направление равнодействующей плоской системы сходящихся сил аналитическим способом.