Р ешение

Так как в число данных и искомых величин входят действующие силы (постоянные по величине и на­правлению), перемещение точки, начальная и конечная скорости, то применим тео­рему об изменении кинети­ческой энергии точки. Си­лы, действующие на тело в произвольном положе­нии, показаны на рис. 1.68 (G — сила тяжести тела, N — реакция плоскости, Т_тр — сила трения).

Вычислим работы сил, действующих на тело:

(так как N и G₁ перпендикулярны к перемещению точки их приложения).

Составляем уравнение изменения кинетической энергии:

Так как тело опускается без начальной скорости, то v_о = 0, тогда

откуда

Пример 6. Поезд массой т — 3-10⁶ кг движется по прямолинейному участку пути со скоростью 20 м/с. Тор­мозной путь составляет 500 м. Определить время и силу торможения, считая ее постоянной.

Решение

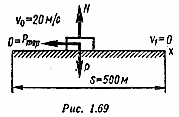
В число данных и искомых величин входят действующие силы (постоянные по величине и направле­нию), время движения, перемещение точки, начальная и конечная скорости, поэтому нужно применить теоремы об изменении количества движения и об изменении кине­тической энергии точки.

Силы, действующие на точку в произвольном положе­нии, показаны на рис. 1.69 (Р — вес поезда, N — реакция рельсов, Р_тoр — сила торможения). Для определения Р_тoр применяем теорему об изменении кинетической энер­гии точки.

Вычисляем работы сил, действующих на точку:

(так как силы Р и N перпен­дикулярны к направлению перемещения точки их прило­жения),

Составляем уравнение из­менения кинетической энер­гии:

где Тогда

откуда

Для определения времени торможения применяем тео­рему, об изменении количества движения точки.

Вычисляем проекции импульсов сил, действующих на точку:

(так как силы Р и N перпендикулярны к оси х),

Составляем уравнение изменения количества движения:

так как

откуда

Пример 7. Груз А массой 3 т и груз В массой т соединены нерастяжимой нитью, перекинутой через блок (рис. 1.70, а). Момент инерции блока относительно оси вращения

где D — диаметр блока. Коэффициент трения между по­верхностями скольжения f = 0,1. Движение системы начи­нается из состояния покоя. Определить скорость груза В и угловую скорость блока после того, как груз В опу­стится на расстояние h. Массой нити и трением в блоке пре­небречь.

Решение

Система состоит из грузов А, В, нити и блока. В число данных и искомых величин вхо­дят: действующие си­лы (постоянные пo величине и направлению), перемещение системы, скорости тел в начале и в конце перемещения. Поэтому для реше­ния задачи применяем теорему об изменении кинетиче­ской энергии системы.

С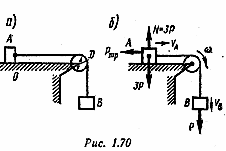 истема в произвольном положении и действующие на нее силы показаны на рис. 1.70,б.

Так как система вначале находилась в покое, то ее начальная кинетическая энергия Т₀ равна нулю. Кине­тическая энергия Т₁ системы при движении груза скла­дывается из кинетической энергии Т_1A груза A, кинети­ческой энергии Т_1Б груза В, кинетической энергии Т_1бл блока.

Вычислим кинетическую энергию системы в момент, когда груз опустится на расстояние h:

где

Выразив угловую скорость блока через скорость груза получим

В ычислим работу сил, приложенных к системе. Работа силы тяжести груза В равна Рh = тgh, работы сил N и 3Р равны нулю (силы перпендикулярны перемещению точки их приложения), работа силы трения равна

Сила натяжения нити является внутренней силой, поэтому ее работа равна нулю.

Таким образом, уравнение кинетической энергии си­стемы в данном случае имеет вид

Отсюда искомая скорость груза

Угловая скорость блока

П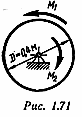 ример 8. В период пуска электродвигателя его ротор вращается под действием постоянного момента М₁ = 80 Н-м. В подшипниках возникает момент сил трения М_{2 =} 5 Н-м (рис. 1.71). Считая ротор однородным диском массой т = 100 кг, определить, сколько оборотов сделает ротор за 6 с после начала движе­ния, и угловую скорость ротора в конце 10-й секунды.