Решение

По за­данному закону дви­жения точки О оп­ределяем ее скорость в момент времени t = 2 с:

при t = 2 с v₀ = 9 м/с.

Цилиндр совершает плоскопараллельное движение. Мгновенный центр вращения находится в точке Р. По­этому

Отсюда мгновенная угловая скорость вращения ци­линдра

Найдем расстояния от мгновенного центра скоростей Р до заданных точек:

Для определения расстояния РН рассмотрим прямоугольные треугольники НКО и РКН. Из

треугольника НКО имеем

Теперь определим величины скоростей заданных точек:

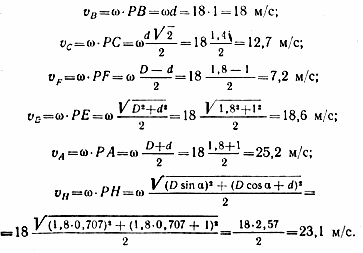
Вектора скоростей показаны на рис. 1.52.

Пример 8. В механизме грохота (рис. 1.53, а) кривошипы O₁А и O₂В связаны звеном АВ. Размеры всех звеньев одинаковы: O₁А = O₂В = АВ = 40 см. Криво­шип O₁A равномерно вращается вокруг оси О_х с частотой п_о = 60 об/мин.

Определить угловую скорость звена АВ и скорость точки В для двух положений грохота:

1) когда кривошип O₁A занимает горизонтальное положение,

2) когда криво­шип O₂В занимает горизонтальное положение.

Р ешение

Вычислим скорость точки А ведущего криво­шипа:

Рассмотрим теперь последовательно заданные положе­ния механизма.

1-е положение (рис. 1.53, б). При заданных раз­мерах звеньев угол АВО₂ = 90°. Определим мгновенный центр вращения звена АВ. Нам известны направления скоро­стей двух его точек: v_A и v_B. Мгновенный центр скоростей лежит на пересечении перпен­дикуляров к направлениям скоростей v_A и v_B, т. е. в точке О₂.

Найдем мгновенную угло­вую скорость вращения зве­на АВ:

откуда

О пределяем скорость точ­ки В:

2-е положение (рис. 1.53, в). Мгновенный центр скоростей в этом положении находится в точке O_v. Мгно­венная угловая скорость вра­щения звена АВ оказывается равной угловой скорости ведущего кривошипа механизма:

Определяем скорость точки В:

Пример 9. Железнодорожный вагон движется по горизонтальному участку с ускорением а₀ = — 1,6 м/с², имея в данный момент скорость v₀ = 1 м/с. Найти уско­рения точек вагонного колеса, лежащих на концах гори­зонтального и вертикального диаметров (рис. 1.54).

Решение

Движение центра колеса О примем за переносное а_е = а₀. Относительное движение является враща­тельным относительно выбранного полюса О. Найдем угловую скорость и угловое ускорение относительного движения.

С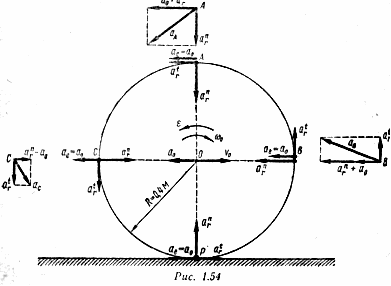 оставим выражение скорости точки О в произвольный момент времени:

Рассматривая движение точки О относительно мгно­венного центра скоростей, который совпадает с точкой Р, найдем угловую скорость вращения колеса:

ω = v₀/OP = v₀/R = 1/0,4 = 2,5 рад/с.

Как известно, v = ωR. Продифференцируем полученное уравнение по времени:

Следовательно, a_t = Rε.

В рассматриваемом примере a_t — касательное ускоре­ние точки О в поступательном движении, т. е. a_t = — a₀ (движение замедленное), ε — угловое ускорение колеса во вращательном движении вокруг точки О.

Тогда

Поскольку все исследуемые точки А, В, Р и С нахо­дятся на одинаковом расстоянии от центра колеса, то относительные касательные и нормальные ускорения их по величине соответственно одинаковы и определяются по формулам:

На рис. 1.54 в каждой точке построены три состав­ляющих ускорения:

Два из трех составляющих векторов для каждой точ­ки направлены по одной прямой и складываются алгебраи­чески. Векторные построения, выполненные на рис. 1.54 около точек А, В и Р, позволяют найти величины и на­правления их абсолютных ускорений: