Решение

1. Разграничим вращательное движение данного тела на участки равноускоренного, равномерного и равнозамедленного дви­жения. Определим параметры вращательного движения тела по этим участкам.

2. Равноускоренное вращение (участок 1):

3. Равномерное вращение (участок II):

3. Равнозамедленное вращение (участок III):

3. Определим полное число оборотов тела за все время вращения:

6. Определим среднюю угловую скорость тела за все время враще­ния:

7. Определим окружную скорость точек тела, расположенных на расстоянии r = 0,5 м от оси вращения через 5 с после начала движения тела:

Пример 8. Диск радиусом R = 2 м вращается вокруг неподвижной оси согласно уравнению

(φ — в радианах, t — в секундах). Определить скорость и ускорение точки поверхности диска в моменты времени t₁ = 0 и t₂ = 2 с.

Решение

Для определения скорости и ускорения точки необходимо знать угловую скорость и угловое ускорение диска.

Уравнение изменения угловой скорости диска:

Уравнение изменения углового ускорения диска:

Определим угловую скорость и угловое ускорение диска в моменты времени t₁ = 0 и t₂ = 2 с:

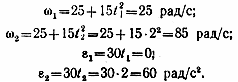
Определим скорость точки поверхности диска в ука­занные моменты времени:

Определим нормальное и касательное ускорения точки поверхности диска в моменты времени t₁ и t₂:

Тогда

П ример 9. Точка А, лежащая на ободе равно­мерно вращающегося шкива, движется со скоростью v = 2 м/с и нормальным ускоре­нием а_п = 5 м/с². Определить ра­диус шкива OA и величину угло­вой скорости (рис. 1.46).

Решение

Здесь для решения следует воспользоваться известны­ми соотношениями для линейной скорости и нормального ускорения точек вращающегося тела:

Если второе уравнение разделить на первое, найдем угловую скорость вращения шкива:

Тогда

Пример 10. Шарик А (рис. 1.47), подвешенный на стержне OA, колеблется в вертикальной плоскости около неподвижной горизонтальной оси О согласно уравнению

(φ — в радианах, t — в секундах).

Определить:

1. Ближайшие моменты времени, соответствующие максимальным отклонениям стержня OA от вертикали OC вправо и влево, а также значение максимальных углов отклонения.

2. Ближайший момент времени после начала движе­ния, при котором нормальное ускорение шарика равно нулю.

3. Ближайший момент времени, при котором касатель­ное ускорение шарика равно нулю.

4. Полное ускорение шарика при t = 1,5 с и угол, образованный вектором ускорения со стержнем OA.

Решение

Стер­жень OA совершает вращательное (коле­бательное) движение. Максимальные углы отклонения стержня от вертикали соот­ветствуют наиболь­шим абсолютным значениям функции sin (πt/6). Очевидно, это имеет место при sin (πt/6) = ± 1:

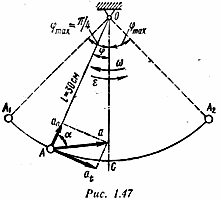
При t₁ = 3 с φ_тах = π/4, при t₂ = 9 с φ_тах = -- π/4.

Крайние положения стержня OA на рис. 1.47 пока­заны штриховыми линиями OA₁ и ОА₂.

Напомним, что за положительное направление считаем вращение по часовой стрелке.

Уравнение изменения угловой скорости стержня OA

Уравнение изменения углового ускорения стержня OA

Направления ω и ε показаны на рис. 1.47. В приве­денном примере направления ω и ε противоположны. Следовательно, стержень OA совершает замедленное вра­щательное движение.

Нормальное и касательное ускорения шарика опреде­ляются по формулам:

В рассматриваемом примере касательное ускорение шари­ка направлено к точке С (рис. 1.47).

Определим момент времени, при котором а_п равно нулю. Для этого выражение а_п приравняем нулю:

Записанное условие выполняется при

но

Тогда

Нормальное ускорение шарика равно нулю, когда стержень OA занимает крайние положения.

Определим момент времени, при котором a_t равно нулю. Для этого выражение a_t приравняем нулю:

Это условие выполняется при

К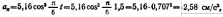 асательное ускорение шарика обращается в ноль в тот момент, когда стержень OA совпадает с линией OC. Вычислим а_n и a_t при t = 1,5 с:

Ускорение шарика при t = 1,5 с

Угол между вектором ускорения шарика и стержнем OA определяется из соотношения

Откуда

Пример 11. Через 30 с равномерного вращательного движения с частотой n₀ = 600 об/мин тело начало равнозамедленное движение и в течение последую­щих 20 с частота вращения тела уменьшилась до n = 450 об/мин.

Определить угловое ускорение тела при равнозамедленном вращательном движении, а также количество оборотов тела за время равномерного и равнозамедленного движения.