Решение

1. Находим модуль равнодействующей. Как известно,

Но если ось х расположить перпендикулярно силам, а ось у — параллельно (рис. 1.47, а), направив ее положительный отсчет вниз, то проекции каждой из сил на ось х равны нулю и, зна­чит,

а проекции сил на ось у равны их модулям с соответствующими зна­ками: F_1y = F₁ = 6 Н; F_2y= F₂ = 8 H; F_3y = F₃ = 10 H; F_4y = F₄ = 15 Н и F_5y = F₅ = 3H.

Таким образом, модуль равно­действующей системы параллель­ных сил

Вектор равнодействующей F_Σ направлен параллельно составляю­щим силам в сторону положитель­ного отсчета оси у, если XF_ky > 0, и в сторону отрицательного отсчета, если ΣF_ky < 0.

В данном случае F_Σ = ΣF_к = 6 — 8 + 10 + 15 — 3 = 20 Н, т. е. равнодействующая равна 20 Н и направлена вниз.

2. Изобразим эту равнодействующую условно штриховой линией на некото­ром расстоянии х от начала координат (рис. а) и запишем моменты всех сил относительно точки Ах'

И, согласно теореме Вариньона, получим

— F_Σx = F_{2 *} A₁A₂ – F_{3 *} A₁A₃ – F_{4 *} A₁A₄ + F_{5 *} A₁A₅

Отсюда после подстановки известных числовых значений сил и плеч —20x = 8 – 0,2 — 10 – 0,4 — 15 – 0,6 + 3 – 0,8, получим

Следовательно, F_Σ = 20 Н, а ее линия действия, параллельная составляющим силам, проходит от точки A₁ на расстоянии l = 0,45 м (рис. 1.47,6).

И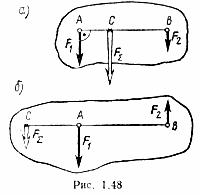 звестные из физики зависимости, возникающие при сложении двух параллельных сил, можно получить из теоремы Вариньона.

Даны приложенные к телу параллельные силы F₁ и F₂, направ­ленные в одну сторону. Согласно равенству F_Σ = ΣF_k ясно, что в данном случае

а вектор равнодействующей F_Σ, приложенный в некоторой точке С, направлен параллельно силам в ту же сторону.

Возьмем сумму моментов сил относительно точки С (точки, че­рез которую проходит линия действия равнодействующей). Тогда

и, следовательно,

или

отсюда получаем известную из физики пропорциональную за­висимость:

т. е. расстояния от линии действия двух параллельных сил до ли­нии действия равнодействующей обратно пропорциональны силам.

Легко доказать (проделайте это самостоятельно), что такую же за­висимость получим и при опре­делении равнодействующей двух параллельных сил, направленных в противоположные стороны, хотя в этом случае модуль равнодейст­вующей F_Σ = F₁ — F_2. Направлена она в сторону большей по модулю силы, и линия ее действия распо­ложена не между слагаемыми силами, а за большей из них (рис. б).

Центр параллельных сил

З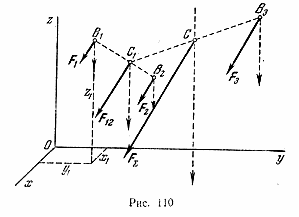 ная правила сложения двух параллельных сил, не­трудно путем последовательного сложения найти равно­действующую и для любой системы параллельных сил.

Пусть, например, к телу приложены в точках B₁, В₂ и В₃ три параллельные и направленные в одну сторону силы F₁, F₂ и F₃ (рис. 110). Сложив сначала по соответствую­щему правилу две силы F₁ и F₂, найдем их равнодейст­вующую F₁₂. Складывая затем по тому же правилу силу F₁₂ с силой F₃, найдем равнодействующую F_Σ всех трех данных сил. Эта равнодействующая, очевидно, парал­лельна данным силам и направлена в ту же сторону.

Модуль равнодействующей равен сумме модулей состав­ляющих сил;

Остается определить положение точки С, через кото­рую проходит линия действия равнодействующей. За точку приложения равнодействующей, конечно, может быть взята любая точка, лежащая на линии ее действия, но оказывается, что только одна из них, именно точка С, определенная путем последовательного сложения сил, обладает особым, весьма важным свойством.

Свойство это состоит в том, что если мы повернем все данные силы вокруг их точек приложения на одина­ковый угол, не нарушая их параллельности, то линия действия их равнодействующей, повернувшись на тот же самый угол (как показано на рис. 110 штриховыми ли­ниями), будет вновь проходить через точку С.

Точка С носит название центра системы параллель­ных сил.

Из сказанного выше следует, что центром данной си­стемы параллельных сил называется точка, через которую проходит линия действия их равнодействующей при любом повороте сил системы вокруг их точек приложения на один и тот же угол в одну и ту же сторону.

Выведем теперь формулы для определения координат центра системы параллельных сил. Возьмем пространст­венную систему осей координат и обозначим координаты точек приложения данных сил: В₁ — соответственно x₁, y ,z₁; В₂ — x₂, y₂ z₂; B₃ – х₃, у₃, z₃.

Координаты центра параллельных сил С обозначим х_С, у_С , z_С.

Как известно, равнодействующей называется сила, эквивалент­ная данной системе сил, т. е. равнодействующая приложенная в точке С, производит на тело такое же действие, как и вся система сил F₁, F₂, . . , F_k, . . ., F_n. Значит, согласно теореме Вариньона, момент равнодействующей относительно любой оси равен алгебраической сумме моментов сил относительно той же оси.

Определим моменты сил относительно оси у.

Так как

где k принимает последовательно значения от 1 до п.

Отсюда

где Поэтому формула для опре­деления абсциссы центра параллельных сил принимает окончатель­ный вид

Определив последовательно момент равнодействующей и момен­ты всех составляющих сил относительно оси х, найдем, что F_Σy_c= ΣF_hy_k, откуда следует формула для определения ординаты цент­ра параллельных сил

Аналогичную формулу для третьей координаты (аппликаты) центра параллельных сил

получим, если повернем все силы на 90°, например так, чтобы они расположились параллельно оси у, и определим моменты сил от­носительно оси х.

Следовательно, формулы координат центра параллельных сил имеют вид

где F_h — модули параллельных сил, x_h, y_k, z_h — координаты точек их приложения.